Formula - Distant and Unusual Galaxies

Hubble's Law - One of the most important formulas of the 20th century. It shows the expansion of the Universe by showing how distant galaxies are moving away from us.
Formula: v = Ho d where:

A rather simple formula for a very important thing, the Universe. Technically, this is a very simplified version of the what the Universe is doing, but it is a good first approximation for what we see in the sky.

Typical Problems

1. Galaxy NGC 123 has a velocity away from us of 1,320 km/s and the Hubble Constant's value is 70 km/s/Mpc. How far away is the galaxy according to Hubble's Law?

Solution: Pop the values into the formula
v = Ho d
1,320 = 70 d
Solve for d
d = 1,320/70
d = 18.9 Mpc

2. Galaxy NGC 2342 has a velocity of 5,690 km/s and is at a distance of 74 Mpc away. What is the value of the Hubble constant based upon these values?

Solution: You can again just pop them into the formula
v = Ho d
5,690 = Ho 74
Solve for Ho
Ho = 5,690/74 = 77 km/s/Mpc

3. Galaxy NGC 4442 is 120 Mpc away. If the Hubble Constant is 68 km/s/Mpc, how fast should NGC 4442 be moving due to the expansion of the Universe?

Solution: Another "pop into formula"
v = Ho d
v = 68 x 120
v = 8200 km/s

Doppler Shift - This formula was originally introduced when light was discussed, but now we're looking at it again. Basically it shows how much light is effected by velocity and allows us (astronomers) to determine velocities based upon the measurable effects.
Formula: v = c x / where:

It should be noted that is the difference or change in the value of the spectral feature from its normal wavelength (), and the change could be positive or negative. If it is positive, the motion is away from you, if it is negative the motion is towards you.
The units you use for velocity and for "c" are sort of arbitrary. Typically for galaxies we tend to use km/s, so the speed of light in this case would be 3.0 x 105 km/s

Typical Problems

1. An absorption feature of calcium usually has a wavelength of 3934 Å, but it is observed in a galaxy to have a wavelength of 4002 Å. How fast is this galaxy moving, and is it moving towards or away from you?

Solution: First you need to determine the value for , which is the change in wavelength
= 4002 - 3934 = 68 Å.
Since this is a positive value, the object is moving away from us. Now you can plug the values into the formula -
v = c x /
v = 3.0 x 105 x 68 / 3934
v = 2.04 x 107/3934
v = 5186 km/s

Redshift - this is sort of like the previous case, except the last steps aren't carried through - the velocity value isn't calculated. There are reasons for that since you may not be able to calculate the velocity using the regular Doppler formula, but may have to use the Relativistic formula (next formula down).
Formula: z = / where:

If we look at the previous formula (Doppler shift), "z" is just the value of v/c, the ratio of the velocity to the speed of light. But as I said, this isn't always correct - there are times when "z" isn't equal to v/c, so it is sometimes easier to just leave it as "z".
And if the value of "z" is positive it is a "redshift" indicating motion away, but it can also be negative, which would be a "blueshift", indicating motion towards us. When dealing with distant galaxies, it is always positive.

Typical Problems

1. An absorption feature of calcium usually has a wavelength of 3934 Å, but it is observed in a galaxy to have a wavelength of 4002 Å. What is the redshift?

Solution: First you need to determine the value for , which is the change in wavelength
= 4002 - 3934 = 68 Å.
Since this is a positive value, the object is moving away from us. Now you can plug the values into the formula -
z = /
z = 68 / 3934
z = 0.017

1. An absorption feature of calcium usually has a wavelength of 3934 Å, but it is observed in a distant galaxy to have a wavelength of 8209 Å. What is the redshift?

Solution: First you need to determine the value for , which is the change in wavelength
= 8209 - 3934 = 4275 Å.
Since this is a positive value, the object is moving away from us. Now you can plug the values into the formula -
z = /
z = 4275 / 3934
z = 1.09
If you put this into the Doppler Shift formula above (using z = v/c), you'd get a velocity = 1.09 c, 9% greater than the speed of light, and that isn't possible!

Relativistic Redshift - This is used in place of the Doppler formula when the velocities become too large to be accurately represented by the regular Doppler formula, typically any velocities greater than 10% the speed of light.
Formula: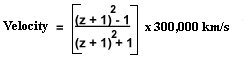
where:

This looks rather complicated, and it is, but it does accurately calculate the velocity of very fast objects without breaking the speed of light rules.

Typical Problems

1. For the problem in the previous example, what is the velocity of the galaxy, whose z=1.09?

Solution: Only one number to put in, but you have some squaring and addition/subtraction to keep track of
v = [(z+1)2 -1]/[(z+1)2 +1] x 300,000 km/s
v = [(1.09 + 1)2 - 1]/[(1.09 + 1)2 + 1] x 300,000 km/s
v = [(2.09)2 - 1]/[(2.09)2 + 1] x 300,000 km/s
v = [4.37 - 1]/[4.37 + 1] x 300,000 km/s
v = [3.37]/[5.37] x 300,000 km/s
v = 0.628 x 300,000 km/s
v = 188,000 km/s

2. You've discovered a new quasar. A hydrogen feature that should appear at a wavelength of 912 Å is seen in the quasar's spectrum to appear at a wavelength of 10,320 Å. What sort of redshift and velocity does this quasar have?

Solution: First you need to determine the value of z. And to do that, you need to determine the value of = 10,320 - 912 = 9408Å.
Now determine the value for z
z = /
z = 9408/912 = 10.3
Now put that into the relativistic formula (why can't you put it into the regular Doppler formula?).
v = [(z+1)2 -1]/[(z+1)2 +1] x 300,000 km/s
v = [(10.3 + 1)2 - 1]/[(10.3 + 1)2 + 1] x 300,000 km/s
v = [(11.3)2 - 1]/[(11.3)2 + 1] x 300,000 km/s
v = [128 - 1]/[128 + 1] x 300,000 km/s
v = [127]/[129] x 300,000 km/s
v = 0.984 x 300,000 km/s
v = 295,000 km/s
Which is pretty darned fast!