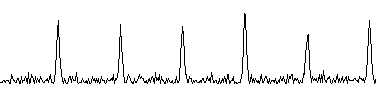
 Figure 1.
A typical pulsar signal, as picked up by a radio telescope.
Figure 1.
A typical pulsar signal, as picked up by a radio telescope. What does a supernova leave behind? That sort of depends upon the size of the original star. Remember, mass determines everything about the life of a star - so here's another example of that rule. In the case of massive stars (those that die via the Type II supernova mechanism), there are two likely possibilities - a neutron star or a black hole. We'll look at the less extreme case of the neutron star first.
If you recall from the discussion of Type II supernovae, the core of the star collapses to form a big ball of neutrons, what we would call a neutron star. This ball of neutron degenerate material is packed in so tightly that a teaspoon of neutron star material would weigh as much as a mountain. The cores of some massive stars end up as neutron stars, and this is where things get tricky. A neutron star is so small (only about 20 km in diameter), so it was thought unlikely that such an object would be visible even using the most sophisticated telescope. People had theorized about the existence of neutron stars since the 1930s, but because of their small sizes, people thought they would only be theoretical objects that could never be detected.
Let's turn the clock back to 1967. Over in England, the Cambridge University Radio telescope project was in progress. While this did not involve what we would call a really sophisticated set up, it was able to do the job. Basically the telescope was a large array of wires spread out over 4 1/2 acres, kind of like a great big wire clothesline strung out over a field. It was just a bunch of wires on posts, so the telescope could not be aimed or moved. How did it look at the sky? The rotation of the Earth allowed the telescope to look in different parts of the sky over the course of a day - though there weren't many places it actually could look - it just pretty much scanned the same strip in the sky day after day.
A graduate student, Jocelyn Bell, was looking at the radio signals coming from the telescope and she noticed that a strong radio signal occurred when the telescope was aimed at certain regions in the sky. The telescope pointed in that same direction each day, and she noticed that the signal reappeared not 24 hours later but 23 hours and 56 minutes later. The signal was detected four minutes earlier each day. What does that mean? Remember, the time for the rotation of the Earth (the sidereal period) is 23 hours, 56 minutes, so sources in the sky will reappear four minutes earlier from the previous day's observation. This told her that the object giving off the signal was up in the sky. It took her a while to convince her boss of the source of the signals - he thought they were from an Earth based source, like telephone lines or radio transmitters. Eventually he was convinced and they started to examine the signals more closely.
 Figure 1.
A typical pulsar signal, as picked up by a radio telescope.
Figure 1.
A typical pulsar signal, as picked up by a radio telescope.
They noted that the signals were not a continuous radio signal (like a steady humming noise) but actually a bunch of individual radio "pulses" (like a heart beat). The pulses were very rapid, so they often had the appearance of a steady, sustained signal. The timing of the pulses was pretty precise - very little deviation from one pulse to the next. Due to the pulsed nature of the signals, the objects were initially called Pulsars.
What exactly are pulsars? Believe it or not, at first they did think
the signals were from extraterrestrials due to the very precise nature
of the pulses, but later trashed this idea when they discovered a wide
range of pulse periods (the time between each pulse) located in many
different directions in the sky. If these were alien beacons, they
certainly didn't appear to be very useful.
| A sound file of a typical pulsar (1.4 pulses/second) | A sound file of the Crab Pulsar (30 pulses/second) | A sound file of a fast pulsar (642 pulses/second) |
What type of object gives off periodic signals, or changes its energy output in a periodic manner? Eclipsing stars can do that. You could get periodic signals from an eclipsing system, but since the signals from the pulsars had periods on the order of one second, that would mean stars would have to be moving around in orbits once each second - that is just a little too fast to be possible, so that idea was scarped.
What about stars that actually pulsate? Remember, the Sun has periodic vibrations, and there are many types of stars that do pulsate. We run into that annoying problem of the period of variation being pretty fast. If a star were to pulsate at the rate of one pulse each second, it would be wobbling so much it would rip itself apart. Again, the pulses are just too fast to be this option.
What else do we have that is periodic in nature? You probably remember that stars also rotate. If a star had an unusual feature on its surface then that feature would appear each time the star rotated toward you, sort of like a lighthouse beacon. This scenario is possible. What type of star could rotate around at a rate of about one rotation per second?
Could a Main Sequence star do it? No, it would tear itself apart. What about a white dwarf? No, it would still have to rotate too fast for it to survive. We need a star that is very small and very dense so that its self-gravity (what's holding it together) could withstand the strong rotation (what's ripping it apart). What sort of object would be appropriate to be a pulsar? What could it be; I wonder, could it be...a neutron star?
It seems that the only object that has enough self-gravity to hold itself together while it rotates at very high speeds would have to be a neutron star - very small, very dense, but able to handle the difficult job. It looks like that pretty much answers the question - or does it? Just because we think that a neutron star is the source of the radio pulses doesn't actually prove that it is cause. As with anything in science you need to get evidence to support the idea. Science involves doing tests and finding evidence - sort of like detective work. Now comes the difficult part, since it is unlikely that we can actually "see" a neutron star directly with a telescope to test this theory (remember how small its diameter is). How do we find the evidence?
If you remember, we thought that neutron stars were produced in a supernovae explosions. We need to link a supernova with a pulsar. If we take a closer look at one of the signals that was discovered very early, you will notice that it is originating from a gas cloud known as the Crab Nebula, which is located in the constellation of Taurus the Bull. Observations of this cloud show that it is changing at a fast rate - it is expanding pretty quickly. It is also a strong x-ray source as well as a strong radio light source. Astronomers thought that it was a supernova remnant. Why do you suppose they thought that?
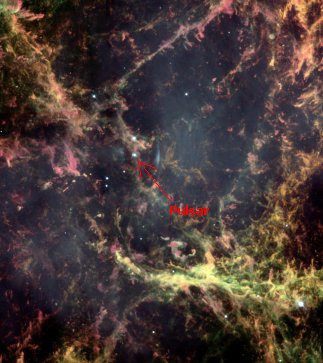 Figure
2. An up close image of the Crab Nebula obtained by the Hubble Space
Telescope. The pulsar is indicated. Credit: NASA and The Hubble
Heritage Team (STScI/AURA).
Figure
2. An up close image of the Crab Nebula obtained by the Hubble Space
Telescope. The pulsar is indicated. Credit: NASA and The Hubble
Heritage Team (STScI/AURA).
Astronomers took a look at historical records that tell us that something happened there many years ago. Observations made in July of 1054 AD indicated that a bright object appeared in the sky. Just how bright was this object? It was brighter than Venus! It was so bright that it was even visible in the daytime for quite some time. Observations of the object were made by the astronomers in the Far East (China and Korea) as well as Arabic astronomers. It seems that the Europeans were too busy with other things to notice the object, or perhaps they thought that since nothing can change in the sky, it must just be a local event, like a meteor shower. The Far Eastern astronomers were pretty accurate in mapping the object's location, so we know that the bright object appeared in the same spot of the sky where we now see the Crab Nebula. Also, the brightness measurements that were made follow the brightness variations of a supernova (a Type II supernova, in fact).
There's the smoking gun. A supernova was observed in 1054 AD. Today we look at this same part of the sky and see not only the Crab Nebula (which was discovered long ago) but also a pulsar right in the middle of the mess. The pulsar at the center is a pretty fast spinner, rotating at a rate of 30 times/second. That seems to confirm the theory - a pulsar that is directly related to a supernova, an event that we thought would produce a neutron star, and appears to have done just that. The Crab Nebula pulsar is one of the few that can be seen with a regular visible light telescope. Long ago astronomers surveyed that part of the sky and thought that the star that we now identify with the Crab pulsar was just a chemically peculiar star. It is spinning so fast it is difficult to see the flashes with the naked eye. There are several other supernova remnants with pulsars in them. One, with the exciting name of G11.2-0.3, was recently studied by the Chandra space telescope and might possibly be a supernovae that was observed by Chinese astronomers in 386 AD. You can read about it here. Other pulsars have been discovered not inside of supernova remnants, but close to them. This isn't too surprising since it is thought that the supernova explosion may eject the core. One case where a pulsar appears to have been ejected is also ejecting material of its own, into a long trail into space. You can see multiple images of that pulsar here.
That's the basic upshot (at least once the mystery was solved). Pulsars are rotating neutron stars! Following the standing rule in astronomy, the name is misleading - pulsars rotate, but they don't pulsate! This is probably a good rule about naming things too early - the name stuck before they knew what they were dealing with.
With that mystery cleared up, there are still some questions that need to be answered - namely, why are pulsars rotating so fast, and what is actually causing the pulses?
We'll tackle the easy one first. The fast rotation is due to a rule concerning spinning objects - the conservation of angular momentum. This is a relation between the rate of rotation (how fast it spins) and the distribution of mass in the spinning object (how spread out it is). As the mass distribution changes, the rate of rotation changes. By decreasing the mass distribution (bringing it in closer), you increase the rate of rotation. You may have seen this in the way that an ice skater will spin faster when they bring their arms in. A change of mass leads to a change in the rotation rate. What does this mean for a pulsar?
First of all, pretty much all stars spin to some degree. Remember, the Sun spins around once every 30 days or so. During the supernova event, the massive core collapses in an extreme way. As it collapses (as the mass is brought in), the rotation rate increases. The reduction in size is so great that the rotation rate increases by a drastic amount - thousands of times faster than the previous rate. A star that was spinning around at a rather leisurely pace will end up spinning around very, very fast due to the extreme collapse of the core. I suppose this would be like having an ice skater with 1000 pound arms that are brought in suddenly during their rotation. The skater would probably rotate so fast they'd burn a hole in the ice.
Currently the fastest spinning pulsar that we have detected is XTE J1739-285 (what a lovely name), and is spinning around at 1122 rotations per second. Yes, that's right, 1122 rotations every second! That would make anyone dizzy.
That's one mystery solved, so now we have to figure out what is causing the pulses.
Another thing that stars have are magnetic fields. A weird feature of magnetic fields is that they get very strong when they are compressed. Guess what happens to the magnetic field during the collapse of the star's core in the supernova event? You guessed it, the magnetic field gets compressed. In the case of the formation of a neutron star, the compression is so great that the increase in the magnetic field strength is also incredibly huge.
A neutron star would tend to have a really strong magnetic field - how does that make the pulses? In the neighborhood around pulsars there are charged particles (mainly electrons) that tend to travel along the magnetic field lines. This has to do with the way magnetic fields and electrically charged things interact. These electrons are zooming along the magnetic field lines. As they move along them, they get accelerated (sped up) by the magnetic field, especially near the magnetic poles of the pulsar. It is a strange feature of electrons that when you accelerate them, they give off radiation - synchrotron radiation. I should mention an important aspect of this radiation. Previous to this all of the light (radiation) that we have come across had its origin in objects that were giving off light because of their temperatures. Synchrotron radiation is not produced by heat and therefore is rather unique. We refer to this type of light as non-thermal. We'll run across more non-thermal radiation sources later. Any ways, synchrotron radiation is mainly found in the radio part of the spectrum, which is exactly why Jocelyn Bell and the Cambridge radio telescope detected it. Very few pulsars can be seen with a visible light telescope (only those that are relatively nearby, usually).
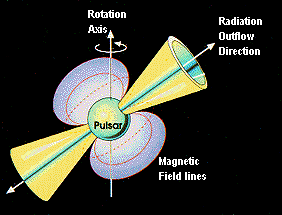 Figure 3.
The model for pulsars. The magnetic field of the rotating neutron star
gives off synchrotron energy. As the magnetic pole sweeps across the
sky, radio light is then sent toward observers in various directions.
This is the classic lighthouse model. You can view a little animation of
a pulsar here. Only when the light source
is directed toward the Earth is the pulse detected. Picture Credit:
NASA.
Figure 3.
The model for pulsars. The magnetic field of the rotating neutron star
gives off synchrotron energy. As the magnetic pole sweeps across the
sky, radio light is then sent toward observers in various directions.
This is the classic lighthouse model. You can view a little animation of
a pulsar here. Only when the light source
is directed toward the Earth is the pulse detected. Picture Credit:
NASA.
Now let's see what we have - a pulsar, spinning very fast, has a whole bunch of radiation coming out of its magnetic poles - so why would that make a pulsed signal? This depends upon the way that the magnetic fields are arranged. The magnetic poles may be arranged in any sort of orientation relative to the rotation of the star. They are not necessarily aligned with the axis of rotation. As the star rotates, the magnetic poles will sweep by, sort of like the way a lighthouse beam sweeps past. These sweeps produce the pulse of light that we detect. Often two pulses are detected from the two magnetic poles, since they cover a good fraction of the star's surface. The high rotation rate of the pulsar makes the pulse very short in duration - now you see it; now you don't.
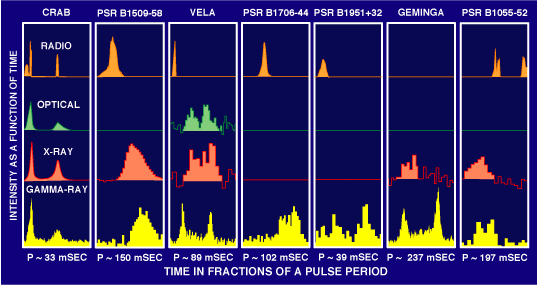 Figure 4.
Light pulses of several different pulsars in different wavelengths. In
some cases pulsars are visible at other wavelengths than radio, the
most common type of signal. Geminga is one of the few pulsars that does
not give off a detectable radio signal, but it does emit x-rays and
gamma rays. The Crab pulsar is one of the few that can be seen in
visible wavelengths. Picture credit: D. J. Thompson, NASA/MSFC.
Figure 4.
Light pulses of several different pulsars in different wavelengths. In
some cases pulsars are visible at other wavelengths than radio, the
most common type of signal. Geminga is one of the few pulsars that does
not give off a detectable radio signal, but it does emit x-rays and
gamma rays. The Crab pulsar is one of the few that can be seen in
visible wavelengths. Picture credit: D. J. Thompson, NASA/MSFC.
That pretty much explains pulsars (which, you remember, don't pulse). There are over 1000 pulsars that have been discovered in our galaxy so far. Most pulse (well, they really don't pulsate, but you know what I mean) at a rate of about 1 pulse/second, though there are some beasts that pulse at rates of over 500 pulses/second. That is a very fast pulse! Pulsars do slow down very slowly, and over time they lose their energy, so eventually they won't be detectable.
There is another interesting aspect about neutron stars - they are neutron degenerate. What does this mean, apart from the fact that they are very dense? It means that if you add mass to a neutron star, it will decrease in radius, just like a white dwarf will shrink in size if you increase its mass. If you have a neutron star in a binary star system and mass is transferring to it, then it would decrease in radius. What happens to a rotating object that decreases its mass distribution (shrinks in size)? You got it - it spins faster. There are actually a couple of pulsars that are spinning faster, and we think this is due to their gaining mass - rather strange, but true. If you thought that pulsars and neutron stars were strange, then just keep reading and learn about some other, even stranger things.
Now if you remember about white dwarfs, they are electron degenerate and they have an upper mass limit (the highest mass that they can have without collapsing in on themselves). Now we just finished off neutron stars, which are neutron degenerate. Does the same sort of rule apply? If so, what would happen to a neutron star if it went over the neutron star mass limit?
The only problem is that the laws of physics that operate on neutron stars are more complicated than those for white dwarfs, so we really don't have a definite answer to this question. Based upon our best ideas about neutron degeneracy we think that there might be a mass limit, like 4 or 5 solar masses. We have seen quite a few neutron stars in binary systems and the masses that we find for them tend to be in the neighborhood of 1.5 solar masses. It doesn't appear that there are very many massive neutron stars out there, which is in line with our theories.
Let's say that there is a massive star out there that is dying and its core mass is pretty large, maybe 6-10 solar masses or so. What does happen if the core of a star is too big to be a neutron star? If it is too big, it has too much gravity, and the collapse will keep going on. Don't forget about what I said about gravity - it rules! If the gravity is too big, then nothing, and I mean nothing, will stop the collapse. We've got something that is getting smaller in size (radius), smaller, smaller and smaller. It's just getting smaller, right? That's no big deal, right? - wrong, wrong, wrong, wrong! Remember the rules for gravity? Remember that the force of gravity depends upon the size of the object - that it goes up strongly for a small decrease in radius. Therefore a big decrease in radius, like that of a collapsing core, would cause a really, really, really huge increase in the surface gravity.
How big is really, really, really huge for surface gravity? What does gravity do any ways? It prevents things from getting away. Let's say you wanted to go to another planet. First of all, you would need to have a rocket that would go fast enough to escape from the the Earth's surface. If the rocket goes just a little bit too slow, it will fall back to the surface of the Earth, which is not a good thing. The velocity that is needed to get away is called the escape velocity, and all it depends upon is the surface gravity of the object that you are trying to get away from. The formula for the escape velocity is
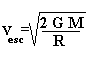
That's a pretty scary formula, but it's not too much different from the gravity formula - the bigger the mass of the object you are getting away from, the higher the escape velocity. The same thing happens if the radius goes down - the escape velocity goes up, so you need to go faster to get away. Just how fast do you have to go? Let's try a few examples. Let's say that you want to leave the Earth (and who doesn't?). How fast would you have to go? - only a measly 11.2 km/s. Does that sound fast to you? Maybe you didn't read that carefully - 11.2 km per second. That's like going across town in one second. You could get a speeding ticket for that, assuming someone could catch you.
We were looking at a collapsing massive star, remember? What happens to the escape velocity when the core is collapsing? It gets larger, right? How much larger does it get? Here are some more examples.
The Sun - it's pretty big, right? To get off of the surface of the Sun (which would probably be a good thing since it is a tad too hot) you would need to move at a speed of 436 km/s. This is like going from Waterloo to Chicago in one second - pretty fast! We can do better - just by decreasing the radius. Let's say that there is a white dwarf. White dwarfs are similar to the mass of the Sun, so the only thing that makes a difference to the escape velocity is their small radius (remember, they're only about the radius of the Earth). To get off of the surface of a white dwarf, you would have to go at about 4700 km/s. How fast is that? That's like traveling across the country in one second.
We can do better than that - go to the next level of extremely small objects with pretty good masses - neutron stars. These little beasts have masses similar to the Sun's, but radii of only about 20 km. The escape velocity gets really, really huge - in this case around 100,000 km/s. This is pretty fast, so fast that you can even describe the velocity in terms of the speed of light - the escape velocity from a neutron star is 1/3 the speed of light. Now that will certainly get you a speeding ticket on the freeway.
Just how small can we make an object (and how high can we push up the escape velocity)? If we make the object smaller in size than the neutron star (but having the same mass, similar to the Sun's), the surface gravity will get bigger and bigger, until...what? The velocity gets up so high that the escape velocity reaches the highest possible speed - the speed of light. When you get to the point where the escape velocity is 300,000 km/s (which is the speed of light), then you have that amazing object known as a Black hole.
 Figure 5.
Albert Einstein - the fellow with the messy hair who gave us the two
theories of relativity. His hair probably had nothing to do with it,
but who knows?
Figure 5.
Albert Einstein - the fellow with the messy hair who gave us the two
theories of relativity. His hair probably had nothing to do with it,
but who knows?
Now a lot of people have really weird ideas about what black holes are and how they act. Don't believe it - they aren't that bizarre. To understand black holes and how they interact with the rest of the Universe, we need to understand some of the rules that are in effect around them, how they influence things (gravity related stuff) and how light operates. These are explained in some of Albert Einstein's theories. Now don't panic - these aren't all that bad, and I'll just go over the basics so that you understand what is going on with them.
First we'll look at the easier of the two theories - the Special Theory of Relativity. I'm not joking about this one being easier - it really is. You've already run into this theory in part, since this is where we get that famous formula E=mc2. That is not the most important part of the theory; it's not even a major component. The main feature of the theory can be stated in the following concept - the speed of light is a constant no matter what is going on, no matter what you are doing, and there is nothing (I really mean nothing) that can travel faster than the speed of light. Now, we already ran over the first part of this when we talked about the properties of light - and actually without that concept the rest of the Special Theory of Relativity wouldn't exist. The second part is sort of like a cosmic speed limit. Nothing goes faster than the speed of light, not even when the cops aren't looking. You might not think that these rules are a big deal, but if you relate it to how things move on the Earth, then it is a big deal.
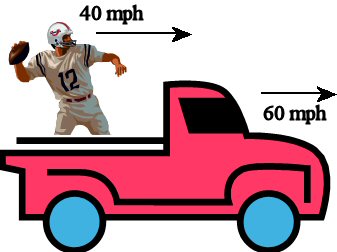 Figure 6. An
example of non-relativistic (low velocity) motion. The final velocity
of the football would be 100 miles/hour (assuming
no air resistance or friction).
Figure 6. An
example of non-relativistic (low velocity) motion. The final velocity
of the football would be 100 miles/hour (assuming
no air resistance or friction).
Here is an example of what I mean. Let's say you have a truck going down the road at 60 mph. In the back of the truck is an overpaid NFL quarterback. He can throw a football with a speed of about 40 mph. Let's say that the truck is going the same direction that he is throwing. Just how fast will the football be moving when it is caught (ignoring the effects of wind resistance and such)? You basically add up the velocities, so the football would be going at a speed of 100 mph. I would not want to be on the receiving end of the toss in this case.
The example illustrated above is pretty straightforward - you just add up the velocities (if they are going in the same direction). What if the quarterback is throwing in the direction opposite of the direction that the truck is going? Then you would subtract the velocities. This is what happens to things going at non-relativistic speeds (speeds much less than the speed of light).
Let's do another experiment, but this time in space. Let's say you have a spaceship going at 1/2 the speed of light (v =1/2 c) - which is within the rules; remember, things can go at speeds less than that of light, so 1/2 the speed of light may seem pretty fast, but it is entirely legal. Let's say in the spaceship is an alien with a laser beam, which is basically just an intense flashlight. Let's say that the alien aims the light in the same direction that the spacecraft is moving. Of course, light from the laser is traveling at the speed of light (v=c). Now let's say we have a detector aimed at the spaceship and the laser, and this detector is measuring the speed of the light coming from the laser. How fast would the light be traveling as we measure it? If you went by the football-throwing example above, you might think that we would measure a speed of 1.5 c (the sum of the two velocities). Unfortunately, that isn't correct. What does the special theory of relativity say? It says that the speed of light would always be c (300,000 km/s) no matter what is going on. Even though the ship is moving at 1/2 the speed of light, the speed we measure for the light will always be c - ALWAYS!!! It doesn't matter if the ship is coming toward us or going away from us; we'd always measure the same speed for the light.
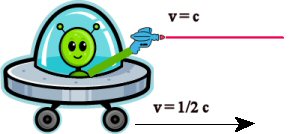 Figure 7. An
example of relativistic velocities. Here the ship is traveling at 1/2
the speed of light (1/2 c), while the light from it travels at the
speed of light (c). Unlike the example shown in Figure 6, you can't
just add the velocities together, based upon Einstein's Special Theory
of relativity. The light coming from the spaceship will always travel
at the speed of light (v=c).
Figure 7. An
example of relativistic velocities. Here the ship is traveling at 1/2
the speed of light (1/2 c), while the light from it travels at the
speed of light (c). Unlike the example shown in Figure 6, you can't
just add the velocities together, based upon Einstein's Special Theory
of relativity. The light coming from the spaceship will always travel
at the speed of light (v=c).
Isn't that just weird? Did we somehow or other lose 1/2 c of velocity? No, we don't lose it, because we can't gain it in the first place. Light is just a rather strange thing. No matter what you do, you can't get a velocity for light greater than c. Don't feel disappointed, because even though we don't get the expected result of adding velocities, we get some other nifty stuff happening. If we were outside of the spaceship watching it go by, and we were to measure the length of the spaceship, we would measure a different length than would be measured by someone in the spaceship or if the spaceship were not moving. If we were to measure the mass of the spaceship from our location, it would be different than if we were in the spaceship or if the spaceship were not moving. If we were to look inside the spaceship at its clocks, we would think they were broken since they would be going at a different rate than clocks not on the spaceship. This is sort of a way that the Special Theory of Relativity makes up for the fact that you don't get the addition of velocities like in the previous example. This also sort of explains why we call it the Special Theory of Relativity - what you measure depends upon your situation relative to the thing you're measuring. If you were on the spaceship and you were measuring things that aren't moving along with you (stuff outside the spaceship for example), you would measure very bizarre things, sort of like the same way someone who isn't moving would be getting strange measurements for the characteristics of your spaceship. You could be moving or the spaceship could be moving - it doesn't matter; the high velocity screws up measurable quantities like length, color, mass, time, etc. The higher the velocity (the closer to the speed of light), the more screwed up the measurements.
Now you are probably thinking that I have to be making all of this stuff up, right? This stuff can't really be happening, can it? Does time really pass more slowly on a fast moving rocket compared to the passage of time on the Earth? Actually, this does happen - and people have checked it out. If you were to put a clock on the space shuttle and let it go around the Earth for a few days, it would not keep time as well as a clock that stayed on the Earth. Even though the space shuttle doesn't go anywhere near the speed of light, it does go fast enough that the effect can be measured on very accurate clocks. These things have been measured - people have put clocks on jets and checked them out. Also, when particles (like electrons) are accelerated in physics labs, their masses appear to change. This isn't science fiction - this stuff does happen.
For the Special Theory of Relativity, just remember, only light goes at the speed of light, it always goes at the speed of light, and if an object goes faster and faster, its characteristics as we measure them will appear to be bizarre. If someone were on an object that is moving very fast, they would think that our characteristics or that of anything not on the fast moving object were screwed up - it's all relative.
Believe it or not, that was the easy theory - now it is time to tackle the much more complex General Theory of Relativity. Actually it won't be so bad, since we're skipping all of the math that goes with the general theory - that's what makes it really nasty. Let's start off with what the General Theory of Relativity does - it picks up where Newton's theory of gravity left off. I'll bet you didn't think that the law of gravity needed any picking up. For the most part it doesn't - the law of gravity as Newton formulated it works just fine for most things. It is in situations where it doesn't work well that Einstein's formula needs to pick up the slack. How does the General Theory do that? It sort of re-defines gravity. You might think of gravity as a kind of rubber band or a glue that makes things stick together (have you ever thought about what actually makes you stick to the surface of the Earth?). Einstein's General Theory re-did gravity by looking at how space (and time) are distorted by mass. Also, if you have distorted space, then the way that mass travels through it will be effected. Basically, mass distorts space, and space effects mass (and anything else within it, like light).
Wait a second, what is this I am talking about? Is distorting space like warping space? It is! How do you distort space? You are familiar with three dimensional space. Any location can be referenced by three coordinates - you can call them x, y, and z, or perhaps latitude, longitude and elevation. No matter how you do it, any location in the Universe can be designated by three dimensional coordinates. Space is three dimensional. Let's distort it - warp it, bend it, and stretch it like silly putty. When space gets distorted, it gets warped into another dimension that we can't see. Let's call this the fourth dimension - this is a dimension of space; it isn't time, that's something else. Where is this fourth dimension? I don't know; I can't show you where it is since we (humans) are only able to exist in and visually comprehend three-dimensional space. You can't point to it, since you can only point in 3-D space, but it is does exist.
Let's see if we can simply things. Think how a flat surface (a two-dimensional surface) can get warped in such a way that it bends into a third spatial dimension. That's how you can have a flat tortilla (two-dimensional object) curved up to form a three-dimensional object (a taco). If we were tiny two-dimensional creatures living on a tortilla, and we were only aware of two dimensions (we could only experience our world in two dimensions), we would not be able to see that the tortilla has been curved into a third dimension, since our senses wouldn't be able to perceive three dimensions. Even if we could "see" the three dimensions of the taco shell, we would be so small compared to the curvature that it would be difficult to detect. This is similar to why you can't easily see that the Earth is a sphere, but that it looks fairly flat to your eyes (after all, we are in Iowa). Going back to your Universe, three-dimensional creatures, like you, me and Einstein, can't see the fourth dimension that space is being distorted into. No matter how badly distorted the space near you is, you can never actually see its curvature. It is also difficult to draw four-dimensional space - frankly, we can't do it. In order to describe warped space we like to simplify things and just use two-dimensional analogies, which we can warp into three dimensions.
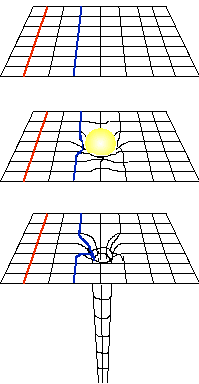 Figure 8. A 2-D analogy to warped 3-D space. The top
view is undistorted 2-D space. The two lines (red and blue) are straight, and
objects moving on them will travel the same distance. Placing a mass in
this space (middle picture) causes the space to distort around the
mass. The larger the mass, the greater the distortion. The red and blue
paths are now no longer equal in length. The blue path is slightly
longer. In the last case, the distortion is very extreme due to a very
massive compact object. Now the differences in the lengths between the
red and blue lines are very extreme. It is even possible that the blue
path has no end but continues down the hole, never ending.
Figure 8. A 2-D analogy to warped 3-D space. The top
view is undistorted 2-D space. The two lines (red and blue) are straight, and
objects moving on them will travel the same distance. Placing a mass in
this space (middle picture) causes the space to distort around the
mass. The larger the mass, the greater the distortion. The red and blue
paths are now no longer equal in length. The blue path is slightly
longer. In the last case, the distortion is very extreme due to a very
massive compact object. Now the differences in the lengths between the
red and blue lines are very extreme. It is even possible that the blue
path has no end but continues down the hole, never ending.
Let's start out with a 2-D universe which doesn't have any distortion, so that it is flat - pretty dull and boring, eh? The rules of General Relativity say that if we were to add some mass to this space, it would get distorted - more mass, more distortion. Let's do that.
Here's the nifty stuff - far away from the mass you do not detect any distortion. The space is just as flat as if you didn't have any mass. As you get closer to the mass, you will experience unusual effects due to the warping of space. Let's say you have two ants in a race in this 2-D universe. They are going to race across the space and travel along straight lines. One will be traveling closer to the mass than the other (one will be along the red line, the other along the blue line in Figure 8). How does the race end? The ant that traveled near the mass had to actually travel along a greater path, since that ant's space was distorted. He lost the race. The weird thing is that he didn't even know that his path was distorted - being a 2-D creature, he could not see the curvature and the line looked straight and normal to him. If the ant had a flashlight (and what well equipped ant doesn't have a flashlight?) then the light from this flashlight would travel along the curved space, but to the ant the beam would be shining in a straight line, as it should. Light, like the ant, must travel in the space that comprises this universe, so it will travel along what is really a curved path. Even though light travels in a curved path, it will always appear to be straight as seen by the inhabitants of the space.
If you really want to see major distortions you'll need to add a large amount of mass. You could also concentrate the mass into a really small space - make it very dense. This is such a strange concept, this warping space stuff, that it might be hard to believe. Believe it or not, any mass will distort space - you are distorting space, the computer is distorting space, the building you are in is distorting space, and even your nose is distorting space (not a great deal, but it is still distorting space).
This sounds like a bunch of science fiction; does this stuff really happen? To test this out, you need to have a large mass. The largest mass object in our neighborhood is the Sun, and we know that it distorts space. One way that this is apparent is in the way that Mercury's orbit about the Sun is gradually altered (orbital precession is the term). When Mercury gets really close to the Sun (when it is at perihelion), it is in slightly distorted space. Its orbit is shifted a little bit. Over the years this alteration to the orbit of Mercury was noticed by astronomers. Newton's laws (and Kepler's laws) could not explain this apparent aberration in the motion of Mercury, and this caused some people to suspect that there was another planet close to the Sun that was messing up Mercury's orbit. This isn't actually the case, but that didn't stop people from trying to find the mythical planet Vulcan (yes, they really did refer to it as Vulcan). Of course, when Einstein came along with his General Relativity, this pretty much explained the problem with Mercury.
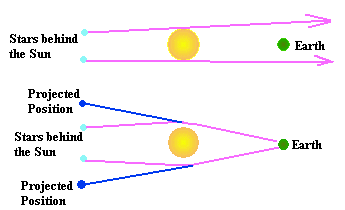 Figure 9. The way that the space around the Sun is
warped. In the top image there is no warped space. In this case, the
stars located behind the Sun could not be seen on the Earth, since the
light from these stars will never reach the Earth. This is not the case,
however. The lower image shows how the space actually alters the path
of light, so that the stars are visible from the Earth. However, since
we can't "see" the warped space, we think the stars are actually in the
wrong positions (the dark blue spots). The positions of the stars that
are lined up with the Sun appear to be off their proper locations by a
small amount, due to their light traveling along warped paths.
Figure 9. The way that the space around the Sun is
warped. In the top image there is no warped space. In this case, the
stars located behind the Sun could not be seen on the Earth, since the
light from these stars will never reach the Earth. This is not the case,
however. The lower image shows how the space actually alters the path
of light, so that the stars are visible from the Earth. However, since
we can't "see" the warped space, we think the stars are actually in the
wrong positions (the dark blue spots). The positions of the stars that
are lined up with the Sun appear to be off their proper locations by a
small amount, due to their light traveling along warped paths.
Is that not enough for you? Here's another instance. Let's say that you have some light traveling near the Sun (light which came from other stars). The space near the Sun is distorted, so the path that the starlight takes will be influenced by this distortion. This was demonstrated soon after Einstein published his theory by astronomers viewing the Sun during a total eclipse. During the eclipse, the locations of stars around the Sun were noted and compared to their normal locations. The star locations were off slightly due to the distortion of space near the Sun. Of course, when we see these stars during an eclipse, we presume they are in the direction in the sky that we see them in, in other words, straight away from us. But those direction are the wrong directions for the star's true location. If space were not distorted by mass, we would always see the stars in their normal locations and Einstein would probably have never gotten that really cushy job at Princeton.
The General Theory of Relatively relates the masses of objects to the effect they have on space. An object like the Sun has measureable effects as described (and tested many, many times) above, but the Earth also warps space. A probe studied the effect of the warping of space by the Earth recently provided evidence that supports the theory. You can learn about the probe and its measurements here.
Einstein's General Theory helped to fill in the gaps that Newton's law of gravity couldn't cover, especially the cases involving extreme masses. It can also be thought of as a way to actually cause gravity. The Earth orbits the Sun due to gravity, right? What if you consider the fact that the Sun is warping space and the planets move in that warped space in the only way they can, like a marble rolling around the inside of a bowl? - the orbits of the planets can be explained by having the Sun's warping of space hold the planets in their own areas of curved space. Near the Sun the "bowl" is steeper, so the orbits are smaller and the planets have to move faster so they don't fall in. Further away, the "bowl" is less steep, so the planets don't have to move so fast. Newton's and Kepler's laws can describe the motion, but Einstein's curved space can give us the cause of it. Whether this helps you in understanding gravity or not is up to you; I'm just telling you how it works. I should also mention that one of the other aspects of the General Theory of Relativity is what it does to time - yes, you got it, time passes more slowly near massive objects than it does further away from them. It's another victim of curved space!
That's enough wandering down the confusing path that Einstein gave us - let's get back to black holes. What can become a black hole? The only ingredient that you need is mass, so anything with mass could become a black hole. This includes stuff like the Earth, a pencil, John Goodman and so forth. The only reason that these things don't normally become black holes is that you have to make them dense enough (compact in size) so that their escape velocities are equal to the speed of light. To do that to the Earth you have to crush it down to a size of less than a centimeter. I suppose a chocolate eclair could push John Goodman over the edge, but I could be mistaken.
That's one characteristic of a black hole - it has mass. Does it have anything else? How about size or shape? Technically it can't have any size, since if it did have a size, that would mean it isn't entirely collapsed down to a black hole. That's sort of a confusing argument, but if you don't think about it too much, it does make sense. For something to become a black hole it must collapse down to such a small size that it can't hold itself up, so it has no size. This means that the mass has to be crushed down to an infinitely small point - a singularity, which has no size but does have a measurable mass. If a black hole didn't collapse down to a singularity, then there must be something preventing the collapse - but there is no known force that can overcome the huge gravitational collapse that we run into in these extreme conditions. Black holes have no measurable radii, but do have measurable masses. Of course, if an object has mass, then it has a gravitational pull on anything around it. Now contrary to what you may think, black holes are not magical vacuum cleaners that travel though the Universe sucking everything in sight down their gullets. They have to obey the laws of physics just like everything else in the Universe, so you can determine how much gravitational pull a black hole has on objects near it. For objects further away, the gravitational pull is much less (just like it is for anything in the Universe). At large distances there would be no problem in escaping from a black hole, so if you ever do run across one in your travels, don't go in for a closer look - you need to stay far away, where the gravitational pull is low. As you'll see, if you do get too close, there will be nothing to save you.
A black hole has to obey the laws of physics, so there is that rule about escape velocity - the speed needed to escape from an object - that you have to watch out for. If you are too close to an object, you need to travel at a very great speed to escape. If you start out at a point further away, the velocity you need to escape is much less. In the case of the black hole you can use this to define a "boundary" for the black hole. There is a distance from the black hole (the singularity) where the escape velocity equals the speed of light. This distance from the singularity is known as the Schwarzschild radius (Rs). This is often referred to as the "radius" of the black hole, since its true physical radius has no size. You can also think of this radius as the "point of no return." If you were closer to the singularity than Rs you would have to travel at a speed greater than that of light to escape, and since nothing can travel faster than the speed of light, nothing can escape from a location within the Schwarzschild radius, not even light (that sort of explains the name "black" hole, doesn't it?). At distances greater than Rs, the gravity is less, so the escape velocity is less than the speed of light, so things like rockets could escape. To give you an idea of how big this "point of no return" is, if you were to make the Sun into a black hole, the Rs would be about 3 km.
The term event horizon is also used to describe the Schwarzschild radius, since that is the closest you can see an "event" happening near a black hole. Anything that happens within the event horizon is not visible since no information can get out of the black hole at that distance. So you could think of it as the last "event" location. In many ways black holes are like Las Vegas - whatever happens in a black hole, stays in the black hole.
The value of the Rs is proportional to the mass of the black hole. A 10 solar mass black hole has a Rs of 30 km, a 1000 solar mass black hole has a Rs of 3000 km, etc. The formula for a black hole's Schwarzschild radius is
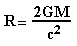
Now I suppose you have been wondering what it would be like to fall into a black hole? Admit it; you've wondered that for a long time. Let's find out.
First of all, we'll start at a great distance from the black hole, where the effect of it on the space around it (the strong spatial distortion as defined by the laws of General Relativity) is pretty low. Far away from the black hole, space and time are not distorted, so things would not appear unusual. We'll leave someone (perhaps a friend of yours) at this location so they can watch you approach the black hole (what a swell friend they are - actually, if they were really a good friend, they'd volunteer to go into the black hole). For your journey into the black hole, you'll have the best equipment - a flashlight and a watch. Obviously no expense was spared for your expedition. You have the flashlight so that you can signal your friend in the spaceship that you are okay, and you agreed that you would signal every 10 seconds (that's why you need the watch). Off you go toward the black hole. Now one of the aspects of General Relativity (and Special Relativity) is that different people in different physical environments (moving and non-moving, and warped space and non-warped space) will measure things differently. There will actually be two different views as to what happens to you as you fall into the black hole. First we'll look at what your friend (or so-called friend who's safely in the spaceship) sees from their position far from the black hole. As you get closer and closer to the black hole, your friend starts noticing some weird things. One is that the signals from the flashlight will become less and less frequent. Perhaps your watch is broken and is running slower than it should - but when the signals start coming at intervals of once a minute, once every 5 minutes, once every half hour, once every hour, once every day...obviously this is not just a case of a broken watch - somehow time is running much more slowly for you (or at least that is what your friend sees). Why? This is one of the connections of space with time - that the space distortions around the black hole also affect the passage of time for different observers. Another thing they'll notice is that the light from the flashlight is getting redder and redder as you approach the black hole. Why? Light is feeling the pull of gravity, but since it can't go more slowly, as other things would, it instead loses energy. Lower energy light has a longer wavelength - so it gets redder and redder as you get closer and closer to the black hole. Eventually the light will be at such a long wavelength that it will not be visible to the eye, since it will be in infrared, microwave and eventually radio wavelengths. In spite of these hardships, your friend (who is probably having milk and cookies in their cozy spaceship) is still able to observe you as you approach the black hole. The time delay gets so extreme that over their lifetime, they don't see you moving any closer to the black hole. Actually, over many generations of people sitting in the spaceship, watching you head toward the black hole, it will look like you are basically frozen near the Schwarzschild radius. To everyone in the Universe, it looks like you don't even get to go across the Schwarzschild radius. As perceived by the rest of the Universe, you're "frozen" on the edge of the black hole.
What will you see? In a way, you see sort of the opposite of what your friend sees. It looks like their clocks are running too fast - and they are moving too fast. Eventually, in what seems like a moment to you, someone on the spaceship will be born, grow old and die right before your eyes. You'll be able to watch the entire life cycle of stars and see them become supernovae. Not only will it look like the passage of time in the Universe is strange, but also the Universe itself will. You will start to see things that were originally not in your line of sight (in front of you). Stuff that was over to the right or left of you would appear to be in front of you - a kind of funneling of light near the black hole. You won't have to turn around to view the entire sky, since it will all be compressed down into a size that you can see. You won't be able to enjoy the cosmic light show for long, since you will cross the Schwarzschild radius, fall into the singularity, and be crushed down to nothingness - ouch.
 Figure 10. An astronaut heads toward a black hole. At
a great distance there is no problem. As the astronaut gets closer, it
gets very uncomfortable, and the tidal forces of the black hole will
stretch him out of shape. It's not the most pleasant way to go, but
what can you do? It should be noted that the diagram isn't to scale,
since the Schwarzschild radius of the 10 solar mass black hole is 30 km
(diameter of 60 km), and the stretching effects don't get really bad
until the astronaut is a few thousand kilometers from the black hole.
Figure 10. An astronaut heads toward a black hole. At
a great distance there is no problem. As the astronaut gets closer, it
gets very uncomfortable, and the tidal forces of the black hole will
stretch him out of shape. It's not the most pleasant way to go, but
what can you do? It should be noted that the diagram isn't to scale,
since the Schwarzschild radius of the 10 solar mass black hole is 30 km
(diameter of 60 km), and the stretching effects don't get really bad
until the astronaut is a few thousand kilometers from the black hole.
That's sort of a sad end, eh? Actually, the end would probably come well before you were anywhere near the Schwarzschild radius. Depending upon the mass of the black hole, you could be ripped apart by tidal forces. What do I mean by this? Let's just put it this way: if you were ever to travel into a black hole or into the general direction of a black hole, you would want to travel sideways, not head-first or feet-first. What difference would that make? Just remember the laws of gravity; anything that is closer to a massive object (be it a black hole, a planet or whatever) feels a stronger gravitational pull than something further away. In the case of a black hole the difference in the pull that your feet would feel and the pull that your head would feel would increase until the part that was closest to the black hole would want to separate from the part that was further away, since it is getting pulled more. You would be basically ripped apart. This is the effect of tidal forces. The less difference in distance between the various parts of your body from the black hole, the less the difference in the pulls those parts would feel. Remember, never go head- or feet-first into a black hole, though in some cases the pulls would be so extreme it wouldn't really matter how you went in, you'd still be stretched like silly putty.
Is a black hole really black? No, not really, because we don't know what color it is. Remember, what your eye perceives as color is just a certain wavelength of light. Light can't get out of a black hole, so the color of a black hole remains unknown. The absence of light from an object would result in the object looking black.
Could a black hole be a passage to another Universe, or just a shortcut into another part of our own Universe? This is sort of the realm of science fiction, but not entirely. We know that black holes severely distort space, so it is possible for it to stretch space from one location to another in our Universe. In a way, a tunnel could be created between different parts of the Universe, though I wouldn't want to travel in that tunnel. Remember, there is a black hole in that tunnel, so it would be easy to get in but not to get out. Such passageways have been proposed by theoreticians and are possible in theory, but whether they exist in reality has yet to be determined. Probably the best kind of tunnel is one that doesn't contain a black hole - though how the tunnel can exist without the black hole is a bit tricky. Just having a nice tube of warped space would be useful for traveling great distances in a short period of time.
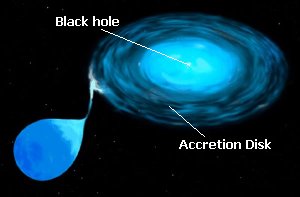 Figure
11. The set up for a black
hole binary. A star, generally a large supergiant, is near an accretion
disk and a black hole. The size of the black hole (maybe only a few 10s
of kilometers) is much smaller than that of the accretion disk (a few
1000s or 100,000s of kilometers in size), so it would be very difficult
to see, even if it were visible to telescopes. The accretion disk
is made up of material sucked off from the normal star (mainly
hydrogen) and gives off x-rays. Credit: Space Telescope Science
Institute, NASA.
Figure
11. The set up for a black
hole binary. A star, generally a large supergiant, is near an accretion
disk and a black hole. The size of the black hole (maybe only a few 10s
of kilometers) is much smaller than that of the accretion disk (a few
1000s or 100,000s of kilometers in size), so it would be very difficult
to see, even if it were visible to telescopes. The accretion disk
is made up of material sucked off from the normal star (mainly
hydrogen) and gives off x-rays. Credit: Space Telescope Science
Institute, NASA.
Are there any black holes out there? How can you tell? Remember, space is black and black holes are black, so how do you find one? You can't see it directly, but you can see it indirectly. A black hole has mass, so it is able to influence objects near it. You would want to look for an unusual binary system. How can you tell if a binary system is unusual? What difference would it make if one of the stars in the binary system were a black hole? First of all, you have to remember about the extreme gravity. Due to this, the black hole may have the tendency to pull material in from the other star. As this material falls into the black hole it will form into an accretion disk (remember how this happens around a white dwarf before it goes nova?). The disk material will be compressed, heated up and basically crunched up even at a great distance from the black hole's Schwarzschild radius. This material (mainly hydrogen and helium from the other star) is heated up to such a high temperature that it will start to give off x-rays. These x-rays are what make the binary system unique. If you were to look at a black hole binary system with a regular visible light telescope, you would probably only see the other star - the normal star. The fact that there is another star in the system, a star that gives off x-rays (actually, the accretion disk around the star is what is giving off x-rays), will make the binary system something that astronomers would notice.
You should be careful about saying whether you have a black hole or not, since x-rays can also come from a binary system that contains a neutron star. The only way that you can figure out which it is (black hole or neutron star) is by determining the masses of the stars in the binary system. And how do you determine the masses of stars in a binary system? With Kepler's 3rd Law, of course (assuming you can determine the size of the orbit and the period of the orbit)! If the mass of the star in the accretion disk is much greater than about 5 solar masses, odds are it is not a neutron star but is instead a black hole. In 2002, there were reports of two very low mass black holes found in separate binary systems; one was only about 4.25 solar masses, and the other was around 5.25 solar masses. These were both discovered in x-ray binary systems with orbital periods of only a few hours!
Another thing that astronomers can look for is how material falls in towards the suspected black hole. When material falls in and lands on a neutron star, it will give off a particular x-ray signal that indicates that it hit something. On the other hand, when material falls past the Schwarzschild radius of a black hole, it just "disappears" - it does not give off a signal indicating any sort of surface or barrier, since there is not one present. Astronomers have carefully looked at the x-rays coming from stuff falling onto neutron stars and stuff going towards a suspected black holes and found very distinct differences between the two - and these matched the models that are based upon the physics involved in these situations.
 Figure 12. Another view of a
black hole in a binary system. If you click on the image you'll see a
small movie showing material flowing into a black hole. There is the
accretion disk around the black hole and also bipolar outflow -
material being ejected from above and below the black hole's location.
This material isn't coming from the black hole itself but is from the
accretion disk. Image and movie from NASA/Honeywell Max-Q digital
group/Dana Berry.
Figure 12. Another view of a
black hole in a binary system. If you click on the image you'll see a
small movie showing material flowing into a black hole. There is the
accretion disk around the black hole and also bipolar outflow -
material being ejected from above and below the black hole's location.
This material isn't coming from the black hole itself but is from the
accretion disk. Image and movie from NASA/Honeywell Max-Q digital
group/Dana Berry.
There are actually quite a few interesting neutron star and black hole binary systems out there. This is only a small sampling of some of the systems -
PSR 1913+16 - This is a pulsar binary system containing two neutron stars - only one of the neutron stars is observed to be a pulsar. The neutron stars are in a very close orbit, so they are moving very fast and this causes the pulsar signals to be distorted. Actually, this type of distortion would happen even if the pulsar were in a regular binary system. What is different about this system is that the distortion of the pulsation periods is also effected by the distortion of space near the neutron stars (General Relativity again rears it ugly head). There is so much distortion of space near this system that the two neutron stars warp each other's space, causing their orbits to continually change. The discovery of this system and its motion over the years provided more support for Einstein's General Relativity (and earned the discoverers the Nobel prize).
PSR J0737-3039A - Like the previous example, this is another binary neutron star system, and in this case both of the objects are pulsars. The orbital period is only 2.4 hours - yes, that's what I said, 2.4 hours. And of course there are also the periods of the pulsars (due to their rotations). One of the pulsars is a milli-second pulsar, spinning around 40 times every second. This is common for binary systems, since any mass transfer will speed up the rotation of degenerate objects. The scientific community was very excited about these two since like the previous example they can be used to test Einstein's theory of General Relativity. There are also all of the neat possible interactions of the two stars' magnetic fields. These stars will eventually merge together and likely end up as a black hole, but that wont happen for another 85 million years.
Cygnus X-1 - This is a very strong x-ray source. However, when you observe it with a regular telescope you see an O type star (named HDE 226868 - isn't that romantic?). The O star is not a source for x-rays, so where are those coming from? You can also see, by looking at the spectrum of the O star, that it is in orbit about something else - something with a mass of about 10 solar masses. If this object were a regular star it should be easily visible. However, it is not - all that is seen is the regular O star. What is 10 times the mass of the Sun but appears to be invisible? - most likely a black hole (it is thought to be too massive to be a neutron star). Cygnus X-1 is the best example we have of a black hole candidate - remember, we only think that it is a black hole; we can't see it directly.
 |
Figure 13. To the left, a view of HDE 226868, a normal star that is also a x-ray source. The x-rays aren't really from the visible star but from an accretion disk around a possible black hole. This is one of the best cases for the existence of a black hole in our galaxy. Images from NASA. | 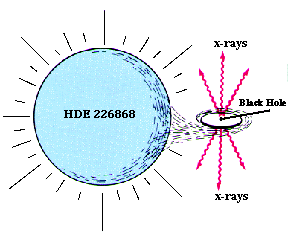 |
Remember, it isn't the black hole that is giving off the energy, but the accretion disk around it. The disk is usually much larger than the black hole itself - a 10 solar mass black hole has a Schwarzschild radius of 30 km, but an accretion disk around it can be over a million km in size. Even if the object itself is not visible, its influence on its surroundings gives it away. There are quite a few objects out there that we think are black holes, but we can't really be 100% sure, since there are always possibilities that these objects are something we haven't yet thought of. Until we know for sure, the really big ones in x-ray binary systems are classified as probable black holes, while those that are less massive are likely neutron stars.
XTE J0929-314 - This is another pulsar, this time in a binary system where it is destroying its companion star. In this case, the pulsar is both sucking material off of the companion star and the strong radiation from the accretion disk is blowing material off of the companion star. These objects are so close that it takes less than one hour for them to orbit one another. The end result is a very rapidly spinning pulsar (185 rotations/second) and a companion star that has evaporated down to the size of a planet (the companion's mass is only about 10 times Jupiter's).
 Figure 14. A
diagram showing what is happening in XTE J0929-314. The pulsar
buried in the accretion disk is pulling material off of the companion
star and also blowing material away. The companion star's mass is
now too small for it to be much of a star. Ultimately there
will only be a neutron star left. Image courtesy NASA.
Figure 14. A
diagram showing what is happening in XTE J0929-314. The pulsar
buried in the accretion disk is pulling material off of the companion
star and also blowing material away. The companion star's mass is
now too small for it to be much of a star. Ultimately there
will only be a neutron star left. Image courtesy NASA.
Some astronomers have been looking for some rather amazing effects caused by black holes, including the triggering of a supernova in a white dwarf. Computer simulations of what happens to a white dwarf that gets too close to a black hole did not just result in the destruction of the white dwarf (which is what was expected) but the ignition of the degenerate material within it due to the strong tidal forces. Just check this article to see results of the study. And even having a normal star getting too close to a black hole can also result in violent supernova-like explosions. It is possible that some of these types of events may have already been observed, as is described in here.
As with many things in astronomy, this is not the last word about how the most massive stars die. Neutron stars and black holes are pretty tricky to observe, so it should not be surprising that there are some other things out there that have only recently been discovered (due to advanced telescopes and observing techniques). One of these weird things is called a Magnetar. This is basically a neutron star with a souped up magnetic field. Now you'll recall that the magnetic field of a neutron star is pretty intense, so having something even more powerful is pretty amazing. To give you an idea of what's involved, here are some facts. The magnetic field of the Earth is around 0.5 Gauss (that's the unit of measure for magnetic fields). A typical refrigerator magnet has a strength of about 100 Gauss. The Sun's magnetic field has a strength of around a few thousand Gauss (remember all those sunspots). A neutron star has a magnetic field with a strength of about 1012 Gauss. A magnetar has a magnetic field strength about 100 times greater than that, around 1014 Gauss. In June 2002, the strongest magnetic field for one of these things was announced - being over 1015 times as strong as the Earth's magnetic field. The magnetic field on a magnetar is so strong that it can cause the crust of the star to buckle and pop every once in a while. This would produce what is basically a starquake, which can be a source of gamma rays. At this point magnetars are pretty rare, since they appear to slow down relatively quickly and lose energy quickly as well. Only a handful of these beasts have been discovered up to this time.
The most recent discovery of a strange object is something that can be called a Strange Star - really, that's what it's called. You can also call them Quark Stars. What's that? You remember that white dwarfs are stars where the atoms are packed as tightly as possible and neutron stars are where the neutrons (a piece of an atom) are packed as tightly as possible. If you break a neutron (or a proton) down, you'd find it is made up of quarks. What if you have an object that is so compressed that the pieces of atoms (like neutrons and protons) are broken down into their smaller bits and those pieces are what make up the star? In that case you would have a Quark Star. Two groups of astronomers in 2002 announced the discovery of possible quark stars - objects that are observed to be too small and cool to be neutron stars. While a typical neutron star should be about 20 km in diameter, these were even smaller.
Magnetars and Quark stars are both extreme cases of neutron stars, though it appears that they are pretty rare at this point. There is some debate as to whether they actually exist; that perhaps the astronomers got their numbers wrong. You'll just have to wait and see.
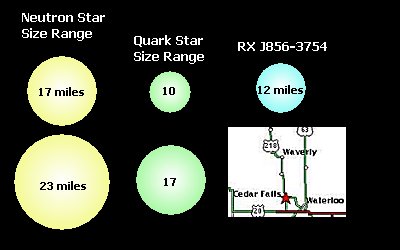 Figure 15. A size comparison of the theoretical size
range for neutron stars (17-23 miles), the theoretical size range for
quark stars (10-17 miles) and the recently discovered possible quark
star, RX J1856-3734. The width of this object (around 12 miles) is
similar to the distance from Cedar Falls to Waverly. Its mass, though,
is likely in the range of 1.5 solar masses.
Figure 15. A size comparison of the theoretical size
range for neutron stars (17-23 miles), the theoretical size range for
quark stars (10-17 miles) and the recently discovered possible quark
star, RX J1856-3734. The width of this object (around 12 miles) is
similar to the distance from Cedar Falls to Waverly. Its mass, though,
is likely in the range of 1.5 solar masses.
Objects like magnetars can be incredibly violent, as witnessed in the spectacular eruption that occured on December 27, 2004. You remember that, don't you? The energy from the magnetar SGR 1806-20, which is a mere 50,000 lightyears away was observed on that day, and this energy release, which lasted about 10 seconds, was brighter than the Full Moon! Surely you remember seeing that? Well, no you didn't see it, since the energy was mainly in the form of gamma-rays. But even though the eruption wasn't visible to our eyes, it was detected by the Swift satellite as well as other telescopes. The energy was equivalent to the energy released by our Sun over 150,000 years. Only recently have astronomers detected some bursts that are even more powerful than this one (see the article about it here). Most likely this will be one of those records that will be broken over and over again.
Gamma-ray outbursts are so energetic that they can be observed from great distances, and as was described previously, we are still not certain how they are produced. In September of 2005 a burst was recorded which was later discovered to have occured from an object that was 13 billion light years away - and in case you were wondering, that is about one of the most distant objects ever observed. This particular outburst, called GRB 050904, was detected by the Swift satellite, and was a very long duration burst. Generally we think that this gamma-ray burst happened when one of the very massive, early stars died and formed a black hole - possibly one of the earliest black holes created in the Universe!
There are some scientists that think that explosions from magnetars or supernovae may have altered or in some cases wiped out life on the Earth in the past. Here is a recent study by some folks that link a mass-extinction that happened 450 million years to a large gamma-ray burst. Such events can severely damage the ozone layer and lead to strong disruptions to the food chain. Of course, this is only speculation, but it does make you wonder what would happen if one of these things went off nearby today.
The area of gamma-ray astronomy is relatively new and astronomers are not exactly sure what the cause or causes of these gamma-ray bursts actually are. As mentioned previously there are several possible causes, including a massive hypernovae explosion, or the collision of objects like neutron stars, or black holes and neutron stars (click here to see an animation showing a black hole shredding and gobbling up a neutron star). Generally it is thought that the end result of gamma-ray bursts are black holes, however this is something that astronomers are still working on, so stay tuned.