Formula:
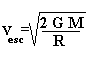
where:
Escape Velocity - How fast must something go (velocity) in order to escape from an object (not fall back down on it). This is used for things like planets, stars, etc., where you need to get your spaceship going a certain speed to "escape". If you don't go this fast, you're doomed to eventually fall back down!
Formula: 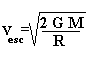
where:
Typical Problems
1. The escape velocity from the Earth is 11,200 m/s. If you want to escape from a planet that has 4 times more mass than the Earth, how fast do you have to go?
Solution: This wouldn't require much work, since you don't have to plug in all the values. A change in M by 4, means that the top part of the formula changes. So an extra factor of 4 is in the part that is being square-rooted.
Vesc = square root (2 G M/R)
Vesc = square root [4 (2 G M/R)]
Take the square root of 4 = 2
Vesc = 2 x square root (2 G M/R)
So you basically have to go twice as fast, or at a velocity of 22,400 m/s.
2. If the planet you are escaping from is 100 times the mass of the earth and 4 times the radius, how fast do you have to go to escape?
Solution: Again, how does the formula change with these changes?
Vesc = square root (2 G M/R)
Vesc = square root [ (2 G M/R ) 100/4]
Vesc = square root [ (2 G M/R) 25]
Take the square root of 25 = 5
Vesc = 5 x square root (2 G M/R)
So the velocity is 5 times the original velocity, or in this case 56,000 m/s.
3. How fast do you have to go to escape from the surface of the Sun? (R = 7.0 x 108 m, M = 2.0 x 1030 kg)
Solution: Well, you'll have to use the ugly version of the formula...
Vesc = square root (2 G M/R)
Vesc = square root (2 x 6.67 x 10-11 x 2.0 x 1030 / (7.0 x 108) )
Vesc = square root (2.7 x 1020/ (7.0 x 108) )
Vesc = square root (2.7 x 1020/ (7.0 x 108) )
Vesc = square root (3.9 x 1011)
Vesc = 620,000 m/s, or 620 km/s
Schwarzschild Radius - the "radius" of a black hole. Not really, it is the distance you have to be from a black hole to escape if you are travelling at the speed of light. Sort of the "point of no return", since if you are any closer to it than this distance, you can't escape. So be careful not to cross the line!
Formula: ![]()
where:
Typical Problems
1. How large is the Schwarzschild radius for a 100 solar mass black hole?
Solution: Using the simpler version
R = 3 M km
R = 3 x 100 km
R = 300 km
2. What is the Schwarzschild radius of the Earth? (Mass = 6 x 10 24 kg)
Solution: You'll have to use the other version of the formula here
R = 2 G M/c2
R = 2 (6.67 x 10-11) (6 x 10 24)/(3.0 x 108)2
R = 8.0 x 1014 / 9.0 x 1016
R = .0089 m, or 8.9 millimeters.