Introduction to Astronomy and Motions of the Sky
What's covered here:
- What is astronomy all about?
- How do objects, like the Moon, Sun, Planets and Stars, appear to move in the sky?
- How do we model the sky, in particular, the positions of the stars?
- Why is the North Star so important?
- How is the sky mapped out and how are locations defined?
- How high above the horizon do objects get?
What's this all about
What exactly is astronomy? What do astronomers study? They
study pretty much everything from the smallest atoms to the entire
Universe. That's a pretty wide field of study, to say the least. They
can do some rather boring things such as using math and physics to
figure out how the Universe and everything in the Universe works - how
things formed, how they move, how they live their lives and possibly
even how they will ultimately be destroyed. They look at how things
move, and unlike meteorologists, they are able to predict things, such
as when the Sun will rise, when the Moon will set or a whole slew of
other things. Some astronomers spend all of their time gathering images
of objects in the sky using a wide range of instruments. Of course,
there is not a lot that they can do on cloudy days - though you'll see
there are exceptions to this rule. Astronomers study such things as
planets, stars, galaxies, moons, asteroids, comets, space dust, gas
between the stars, groups of galaxies, black holes, the shape of the
Universe and ultimately the fate of the Universe.
If you want to really get an astronomer mad at you, just mention
astrology. This will not win you many friends in the astronomical
community. However, like an old skeleton in the closet, we (astronomers)
can't ignore some of the concepts that are usually associated with
astrology. Of course, if you want to make a lot of money from a bunch of
gullible people, become an astrologer - I wouldn't recommend it, but it
can't be denied that astrologers can make some big bucks, mainly because
people are just too easily boondoggled. Just remember, if you ever use
the word astrology in class when you actually should say astronomy, I
just might have to make you stand in the corner.
The history of astronomy is pretty long; in fact, you can think of
astronomy as the oldest of all of the sciences - not to be confused with
the oldest profession! In spite of this long and noble lineage, we can't
ignore the linkage between astronomy and astrology. In fact, in the old
days, astrology was even considered a serious (!) topic of study, along
with astronomy. Both were important, at that time, in trying to figure
out how the sky operates. Why was it important that we knew how the sky
operated?
In the old days, and I don't mean 1974 by "old," before the
invention of such annoying things as digital watches, cell phones and
other modern bits of technology, people's lives depended upon the sky.
Remember, most people in the old days were not formally educated, so
they might not have been able to understand a clock or a calendar
(reading was generally only for the rich and wealthy, and those who
worked for them). Most people lived in an agriculturally based society -
not too different from Iowa, but even more rustic. What does that have
to with astronomy? In those days, it was important to know when to do
things - remember, most of the people wouldn't know a calendar from a
hole in the ground - well, maybe they would if they fell in the hole,
but you know what I mean. Any ways, it was important for the people to
know when to do the things that were vital for their existence.
Since most people were farmers, they needed to know when to do
such important things as plant the crops, harvest the crops, expect the
winter to come to an end, and check to see if you still had enough food
left to survive. These were pretty basic things, and there was no CNN to
tell people what to do and when to do it.
What does planting, harvesting and such have to do with astronomy?
By knowing that a certain constellation was visible in the evening sky
(or the morning sky), people knew it was time to harvest; they knew that
at this time of year, the rivers would tend to flood; or by noting the
position of the Sun at noon in the sky, they knew that it was a month
until the end of the cold weather - killing frosts. Of course, people,
being rather uneducated, were also under the belief that the stars and
planets in the sky would also effect their lives just by their locations
in the sky. Yes, this is what that other "a" word (astrology) is all
about. Since people were so dependent upon the motions of objects and
the predictable patterns in the sky (astronomy) to stay alive, if they
could use another aspect of the sky (astrology) to hedge their bets,
then it perhaps helped them to survive. Generally, astrology never
helped anyone, except for the astrologers who got rich off of all of
the fools that believed them.
Also, other aspects of the sky were important, and are still
important today. Do you know what the phase of the Moon is today? Do you
think that is important? You probably don't think it is, but several
major cultures still use the Moon as a basis for their calendars - these
include people who use the Islamic, Judaic, or Chinese calendar.
That's a pretty large number of people. You still think that you don't
care about what the phase of the Moon is? You don't think it's
important for the typical Iowan? Here's a question - how is the date of
Easter determined? You know it is on a Sunday, but the date changes
from year to year. Why? I'll tell you - it depends upon both the Sun
and the Moon. The day that Easter is celebrated on is the first Sunday
after the first Full Moon after the first day of Spring (also called
the Vernal Equinox). You can go look it up - you'll see that this is
how it is set up! The first day of Spring is based upon the location of
the Sun in the sky, so that and the phase of the Moon determine the
date of Easter.
In the old days, it was important for people to know how the objects
in the sky moved and when they were in certain locations. What are you
going to do if it is cloudy all of the time? How would you know when to
plant your crops if you can't see the stars, the Sun, the Moon, or
whatever object you use as a calendar? What then? This is sort of where
the science (and math) comes in. Astronomers not only can tell where
things are, but are also able to predict where they should be. In this
way, they can tell people when to do their agricultural work at the
right time, regardless of the weather. Here's something you might not
have known - in western Europe, most of the people who did astronomy
(and astrology) were employed by the Christian church, since they needed
to know when various festivals or celebrations had to be held. People
working for the church, such as the priest and monks, tended to be
literate and were able to do complex calculations that showed how the
objects in the sky moved. If you wanted to know when you were supposed
to do various things, you needed to know when things were going to be at
certain locations and to do that you had to figure out how everything
worked - and this isn't easy.
Of course, if you were to make your fortune suckering people with
astrology, then you also needed to know math and the workings of the
sky, since you had to know where things were or will be in the future.
If you can figure out the motions of the planets along with the Moon and
the Sun, then you can really make some serious money in the astrology
trade, so even the non-scientific astrologers did have to know enough
science to cast their horoscopes. Of course, nowadays, astrologers can
be total idiots since a computer can figure out everything for them.
Now that I've convinced you about the importance of astronomy in the
old days and how it used to be linked with astrology, let's just see how
really tricky it is. What were those complicated motions that your
friendly neighborhood astronomer had to predict and understand?
Motions of the Sky
First a word of explanation - when we talk about stuff "rising" and "setting" it is
the appearance of something rising or setting. In reality objects like the Sun or Moon aren't
physically rising from the horizon. Most of the motions we see in the sky are caused
by our (the Earth's) motion, both its rotation and orbital motion. It is just
common to say "the Sun rose in the East today" rather than to say "the Earth rotated toward the
direction of the Sun, which caused it to appear to rise in the east". So all of the
"motions" described below are really apparent motions - not really an
indication of how things are actually moving, but how they appear to move.
Motions/Events of the Sun
The Sun is pretty bright, and without it, all life on Earth would be
nonexistent, so let's see how complicated its motions are. We'll just
consider the motions that you would see in Iowa -
- It rises along the eastern horizon and sets along the western
horizon - but it doesn't rise exactly due east and it doesn't set
exactly due west. The exact location on the horizon where it rises and
sets changes over the months. Another thing that changes is the time of day it
rises or sets. Both of these aspects of the Sun's motion change with the
seasons.
- Actually, there are two times during the year when the Sun does
rise exactly due east and set exactly due west. These times are used to
determine the starts of some seasons.
- The Sun appears to travel along a different path of the sky during the day over
the course of a year. What does that mean? It means that sometimes the
Sun appears very high in the sky and sometimes it appears closer to the
ground - even at noon, it looks rather low. This changes over the course
of the year as well.
- The Sun appears to move pretty fast - it gets back to the same
position in the sky in about 24 hours, but the number of hours that it
is visible varies with the seasons (fewer hours of daylight in winter
and more hours of daylight in the summer, which of course is when it is
visible for either shorter or longer intervals of time. This doesn't
mean that the Sun is actually "moving" faster in the different seasons,
it just means that the path it appears to travel is different in the
different seasons).
- The motion of the Sun across the sky appears to be pretty fast,
but is it really moving? Does it ever move? How can you tell?
- Occasionally there are times when amazing things happen to the
Sun - these are events known as eclipses and these will cause the Sun to
disappear from view for a few minutes.
- If you want to experiment with a simulation showing the apparent motion of
the Sun, just follow this link.
You can change your location on the Earth, as well as the time of the year to see the changing apparent path of the Sun.
(Simulation courtesy of the Astronomy Education at the University of Nebraska-Lincoln Web Site http://astro.unl.edu).
If I were to ask you to come up with a method that would allow you to
determine the exact rise or set time of the Sun for, say, May 17th,
could you do it? This is actually a pretty difficult problem and we
won't tackle it (yes, you can breath a sigh of relief now), but there
are some other things you'll have to predict - just stay tuned.
Motions/Events of the Moon
After the Sun, the Moon is the most obvious thing in the sky. Even on
hazy or semi-cloudy nights, it is often possible to spot the Moon, so
what are its motions that people have to worry about?
- It rises somewhere along the eastern horizon and sets somewhere
along the western horizon, but again not generally in the same place
from one day to the next. Unlike the Sun, there are no special days when
the Moon will rise due East or set due West.
- The time that the Moon rises or sets is not always the same - it
varies; typically it will rise about one hour later each night.
- The path it appears to travel is not the same as the path of the
Sun; sometimes it is on a more southernly path (so it is below the Sun's
path as we view it from Iowa), and sometimes it is on a more northernly
path (above the Sun's path).
- The most obvious aspect of the Moon is its appearance. These are
the phases that the Moon goes through. It takes about one month for the
entire phase cycle to be completed. Why does it do that? Can you predict
the phases?
- The motion of the Moon across the sky is noticeable when you
compare it to the stars - it can be in front of stars of one
constellation during the course of one night, and the next night it will
be amongst the stars of another constellation. It takes about one month
for the Moon to traverse the sky and end up back where it started (back
by the stars that it started out near).
- Like the Sun, there are times when the view of the Moon is
hindered. While in the case of the Sun getting eclipsed the entire Sun
may be hidden, during a Moon eclipse (actually, we call it a Lunar
Eclipse) it still may be possible to see the Moon, but it may be colored
dark brown, red or orange - sort of freaky. Lunar eclipses are visible
more often than solar eclipses by folks in Iowa.
- If you would like to investigate the relative location and motion of the Sun and Moon
together, along with the changing appearance of the Moon, you can follow
this link.
(Simulation courtesy of the Astronomy Education at the University of Nebraska-Lincoln Web Site http://astro.unl.edu).
In a way the motions of the Moon are even more complicated than the
Sun's motions. There are some aspects of the motions that are pretty
easy to understand, as you'll see.
Motion of the Stars
The other main players in the evening sky are the stars, and I don't
mean Brad Pitt or Angelina Jolie, but those twinkly little things in the sky. What
do we know about them just by looking at them with our eyes?
- Stars seem to remain in fixed patterns in the sky, which we call
constellations. They stay in these patterns and don't appear to change
over your life time or the life times of generations. Of course, people
give them names, sometimes silly names, but they do help us find our way
in the sky since they appear to remain in fixed patterns.
- If the stars are in "fixed" patterns that means they don't
move, right? WRONG! They appear to move (while staying in their
constellation patterns) over the course of the evening, as anyone who
has slept under the stars can tell you. If you watch them over the
hours, you will notice that most stars appear to rise somewhere in the East and set somewhere in the
West over the course of an evening.
- You may have noticed that I said that "most stars" appear to rise
and set. This is because not all stars rise or set. Some are visible in
the sky the entire night. Even if you could see them in the daytime, you
would still never see them set. These are the stars that are near the
pole star, the star you may know as Polaris, the North Star (it has
nothing to do with snowmobiles, or a hockey team). Stars that never rise
or set do move, though. If you could watch them move over the course of
an evening, you'd see them move in a circle around Polaris, which
doesn't appear to move at all. These stars, those near Polaris that
never set, are called circumpolar stars.
- Stars rise and set and move over the course of the evening, but
do you always see the same stars (constellations) over the course of the
year? No; you will see different constellations over the course of the
year. The constellations in the early evening sky in January and the
constellations visible in the early evening sky in July are different -
except for those circumpolar stars that never seem to go away.
- If you were to watch one star every night for about a week, you'd
notice that this star would rise earlier and earlier each night. After
many weeks different constellations will become visible in the early
evening sky because of this gradual shifting of the rise time of stars.
- If you would like to investigate the motion of the stars across the sky as you see them,
just follow this link to a Flash simulation where you can add stars and cause the sky appear
to the rotate. You may also want to change your latitude to see how the apparent paths of the
stars change.
(Simulation courtesy of the Astronomy Education at the University of Nebraska-Lincoln Web Site http://astro.unl.edu)
Of course, if you have looked carefully at the stars, you have noticed
that they have different appearances - some stars are brighter and some
are fainter. If you have good eyes and look at stars carefully, you may
also notice that the colors of stars vary - this is particularly easy to
notice with the really bright stars. Some stars are bluish-white, others
are yellow, and others are red.
Motions of the Planets
With your unaided eyes (that means without using binoculars or a
telescope) you can see six planets (can you name them all?). How can you
tell that an object in the sky is a planet and not a star? I'll tell you
after I go over the motions of the planets (yes, I do like to keep my
students in suspense!).
- Like pretty much everything else, planets rise somewhere in the
East and set somewhere in the West. The path they appear to follow is
pretty close to the path that the Sun and Moon appear to follow.
- Not all planets move in the same way. Some are only seen near the
Sun, either around the time of sunrise or sunset (Mercury and Venus are the two that do this). This causes
people to sometimes call them the Morning or Evening Stars. This is
particularly true of Venus, which is the brightest thing up in the sky
after the Sun and the Moon.
- The other planets have some rather interesting motions. Planets
like Mars, Jupiter and Saturn move generally
toward the East compared to the stars over the course of weeks or
months. The animation shows how Mars moves over several weeks' time
relative to the stars.
- The planets don't have a uniform motion. By this I mean they
don't travel amongst the stars with the same speed. Sometimes they move
faster and sometimes they move more slowly. There are even times when
they will stop and then appear to go backwards for a while. This
retrograde motion was one of the really complex problems concerning the
motion of the planets. Why would a planet want to go backwards?
- Here's the really tricky bit - how can you tell the difference
between a star and a planet? You might remember a song that goes
"twinkle, twinkle, little star..." Have you ever heard of a song that
goes "twinkle, twinkle, little planet"? I thought not. That's because
planets don't twinkle. In case you aren't sure, twinkling is the
shimmering or blinking appearance that stars, especially bright stars,
have. Planets don't twinkle, and since the planets that are visible to
the naked eye are pretty bright, you can tell they are planets by not
seeing them twinkle. As long as it isn't an airplane, if it's really
bright and really steady in brightness, then it is probably a planet. As
to which planet it is, you might have to guess or just pick one out of
the air - just make sure you don't tell anyone that it is "Vulcan."
Have you figured out the six planets that you can see with your naked
eye? Did you remember to count the one that you live on?
Models of the Sky - Celestial Sphere
All of the motions that I went through are pretty complex, and they all
need to be explained, so that you can predict the motions, so that you
can set up some sort of calendar system, so that you'll know when to
celebrate your various festivals and celebrations or when to plant or
harvest your crops, or, well, whatever you need to know. To explain all
of these motions, early astronomers/astrologers needed to figure out the
mechanics of the sky - they needed a model (something that could explain
the motion; not necessarily a physical model, but at least something
that they could write down). Since the motions of the stars are fairly
uniform, the model for their motions is easiest to do and we'll tackle
it first. One of the concepts that people believed in the old days was
that the stars (and everything else in the sky) were moving and the
Earth wasn't. This sort of made sense, mainly because people did not
feel any motions from the Earth - they had no sense that it was moving,
like you would feel motion on a ship, a horse or a wagon. Obviously to
these people, the Earth didn't move. Now we know that this idea is
totally bogus, but in the old days it made sense, and it also helped
astronomers to figure out how to make a working model of the sky.
The early, simple model of the sky is known as the Celestial
Sphere. What is it? Basically a big see-through imaginary globe
around the Earth. The stars are stuck on this sphere, and as the sphere
spins around, the stars would move with it. This really explains how
the stars move pretty clearly, since they are on this spinning globe,
those near the axis of the rotation, like near the North Star, would make little circles around
the pole star, while those further from the pole
would move along larger paths across the sky. If you don't get this
idea, think about how an umbrella looks as you spin it around above you.
If you have a bunch of spots on the inside of the umbrella, the spots
far from the handle will make large circles around as you rotate the
handle, while those near the handle will make little circles. If you
were to take the ends of the umbrella and stretch them around you would
have a sphere, just like a Celestial Sphere surrounding the Earth.
People thought that the stars' patterns never changed (they stayed in the
same constellation patterns) since they were all "stuck" on this big
sphere. Stars also never appeared to change their appearances, their
colors or their brightnesses - at least not in a way that was
noticeable. By putting them on a fixed, big sphere, people sort of made
them eternal. The worst part of it all is that this model worked really
well! BUT IT IS TOTALLY COMPLETELY WRONG!!! One of the obvious
problems is that it implies that all of the stars are at the same
distance from the Earth, and this is not correct. Even though this model
of the sky is not correct in terms of the real Universe, it is useful
in determining positions of objects and defining a coordinate system of
the sky. Just remember - IT IS WAY WRONG!!!!
What is it? Basically a big see-through imaginary globe
around the Earth. The stars are stuck on this sphere, and as the sphere
spins around, the stars would move with it. This really explains how
the stars move pretty clearly, since they are on this spinning globe,
those near the axis of the rotation, like near the North Star, would make little circles around
the pole star, while those further from the pole
would move along larger paths across the sky. If you don't get this
idea, think about how an umbrella looks as you spin it around above you.
If you have a bunch of spots on the inside of the umbrella, the spots
far from the handle will make large circles around as you rotate the
handle, while those near the handle will make little circles. If you
were to take the ends of the umbrella and stretch them around you would
have a sphere, just like a Celestial Sphere surrounding the Earth.
People thought that the stars' patterns never changed (they stayed in the
same constellation patterns) since they were all "stuck" on this big
sphere. Stars also never appeared to change their appearances, their
colors or their brightnesses - at least not in a way that was
noticeable. By putting them on a fixed, big sphere, people sort of made
them eternal. The worst part of it all is that this model worked really
well! BUT IT IS TOTALLY COMPLETELY WRONG!!! One of the obvious
problems is that it implies that all of the stars are at the same
distance from the Earth, and this is not correct. Even though this model
of the sky is not correct in terms of the real Universe, it is useful
in determining positions of objects and defining a coordinate system of
the sky. Just remember - IT IS WAY WRONG!!!!
The constellations that the stars are associated with used to just
be traditional groupings. Different cultures had different
constellations. When astronomy got more scientific and organized, the
little stick figures you see for the constellations sort of changed over
time. Today there are 88 constellations in the sky and they are actually
sort of like counties in a state. There are 99 counties in the state of
Iowa and each piece of land in the state is part of some county, based
upon where the boundaries are drawn. This is also how we now divide up
the sky - the constellations don't just define a stick figure of a dog,
horse or person, but a region of the sky. Something in that region
belongs to a certain constellation. This is shown in Figure 1.
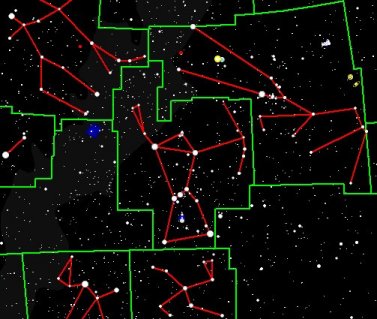 Figure 1. The
territory that belongs to a certain constellation is shown by the
green lines, while the red lines show a traditional way of drawing the
"shape" of the constellation. The constellation boundaries are not
subject to change, but the lines that represent the stick figure for the
constellation can be drawn in any sort of pattern.
Figure 1. The
territory that belongs to a certain constellation is shown by the
green lines, while the red lines show a traditional way of drawing the
"shape" of the constellation. The constellation boundaries are not
subject to change, but the lines that represent the stick figure for the
constellation can be drawn in any sort of pattern.
Even though the Celestial Sphere is not a real model of the sky, it
is useful for mapping out locations of objects in the sky. The
Celestial Sphere was set up so that it used some of the coordinates that
are used on the Earth. Remember, the Earth was thought to be at the
center of the Celestial Sphere, so it wasn't too difficult to extend
the Earth's coordinates to the sky. Putting the Earth in the middle of
everything may seem egotistical, but there were other reasons for doing
it. Figure 2 shows the basic set up for a Celestial Sphere. There are a
couple of special locations that need to be pointed out.
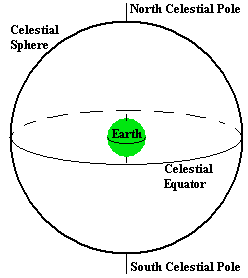 Figure 2. The
Celestial Sphere, an imaginary ball around the Earth upon which the
stars were thought to be located. This is not true - the stars aren't
on this sphere, but it does provide an easy way to map out the sky.
Figure 2. The
Celestial Sphere, an imaginary ball around the Earth upon which the
stars were thought to be located. This is not true - the stars aren't
on this sphere, but it does provide an easy way to map out the sky.
Celestial Poles - these are points on the Celestial Sphere
that are directly above the Earth's Poles, so there is a Celestial North
Pole and a Celestial South Pole. You can also say North Celestial Pole
and South Celestial Pole; it doesn't really matter how you say it.
Celestial Equator - this is just a line that is directly above
the Earth's Equator. Like the Earth's equator, the Celestial Equator
goes all the way around the Celestial Sphere.
We need to simplify some locations in the sky now. We can talk about
stuff that is directly over head, or we can say stuff is at your zenith - this just means the location
right over your head. You have a personal zenith and what is there
depends upon where you are on the Earth, what time of day or night it is
and what time of the year it is. There is also a term for the exact
opposite of zenith, but we don't really care about that since it would
be in the direction of the ground and there are no stars visible down
there.
Another special direction is the horizon, though that is not
really one particular direction, but sort of, well, your horizon. To be
kind of technical, the ground meets the sky at the horizon, and
generally, there are 90º between the horizon and the zenith
(especially in Iowa). If you do want to get specific about the horizon,
you could say the southern horizon, the northern horizon, etc.
Here's a rather surprising concept that you might not have known
about - the ancient astronomers did not, I repeat, NOT, believe that the
Earth was flat. In fact, it was pretty much agreed that it was
spherical, though the size of the sphere was so big that to us puny
humans it looked like a flat surface. Actually, as you'll see, ancient
astronomers were sort of fixated on everything being spheres. We'll get
to that later.
As previously mentioned, the Celestial Sphere was useful for finding
your way about the sky, since like on a globe of the Earth you can
designate various coordinates to measure locations or positions of
objects. First, we'll tackle the north-south coordinate system. On the
Earth, the amount that you are north or south of the Earth's equator is
measured in degrees of latitude. There are certain special locations on
the Earth. If you are at the Equator, you are at a latitude of 0º;
if you are at the North Pole, you are at a latitude of +90º
or 90º North (this is the highest possible value) while at the
South Pole your latitude would be -90º or 90º S.
We're not at one of those locations - we're in Cedar Falls (at least
I am). How do we determine our latitude? Simply draw a line from our
location to the center of the Earth and a line from the Equator to the
center of the Earth (see Figure 3). Now measure the angle between these
two lines - this is our latitude! For Cedar Falls, our latitude is 42.5º
N. The latitude of any location on the Earth can be found by
measuring its angular distance from the Earth's equator. Draw a line
from the North pole to the center of the Earth and you'll end up with an
angle of 90º - which is the latitude of the North pole!
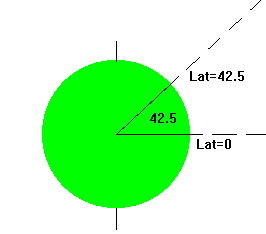 Figure
3. The definition of latitude. The angle between your location and
the equator (where latitude =0) determines the value of your latitude.
Figure
3. The definition of latitude. The angle between your location and
the equator (where latitude =0) determines the value of your latitude.
Now, if we were to take this coordinate system and stretch it up to
the sky, we would be cooking! Why can we do this? First of all, the
Celestial Sphere is already sort of set up the same way as the latitude
system - there is a Celestial Equator and there are Celestial poles.
Just extend the latitude system to the Celestial Sphere to get the
angles that objects are North or South of, not the Earth's equator, but
from the Celestial Equator. We can't call this system latitude, since
that name is already taken. Instead, this coordinate system is known as declination (abbreviated as dec). Declination is just the angle
an object on the Celestial Sphere has as measured from the Celestial
Equator, just like latitude is the measure of the angle between an
object on the Earth's surface and the Earth's equator.
One really neat thing about this system is how declination and
latitude are linked. An object at your zenith (remember, that is right
over your head) will have a declination value equal to your latitude! If
you are located on the Earth's equator (0º latitude), at your
zenith would be a declination of 0º (which is the declination of
the Celestial Equator). If you are at the North pole, you are really
cold, and your latitude is 90º N. If you don't freeze to death,
you might notice that at your zenith is a declination of 90º N. If
you are in Cedar Falls, 42.5º N latitude, then at your zenith is a
declination of, you guessed it, 42.5º N. Check out Figure 4 to see
this sort of arrangement.
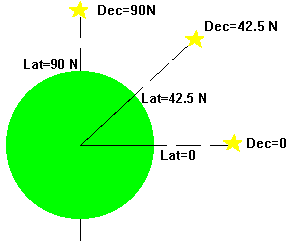 Figure 4. How
declination and latitude are related. An object at your zenith has a
declination value that equals the value of your latitude.
Figure 4. How
declination and latitude are related. An object at your zenith has a
declination value that equals the value of your latitude.
Just like latitude, declination is measured in units of degrees. The
two extremes are at the North and South Celestial poles: +90º to
-90º respectively (or you could say 90º N and 90º S). You
can't have a declination greater than +90º or less than -90º!
Sometimes a degree is pretty big and you need to measure an angle
that is much smaller than a degree, so you need to use a smaller unit of
measure (sort of like the way an inch is a smaller unit of a foot). To
make life easier, we can divide one degree into smaller units known as minutes. To be precise, 1º =
60' (the dash stands for minutes). Sometimes using minutes is not
enough; even smaller units are needed. We can divide each minute up into
(you guessed it) seconds. Of
course, the division is 1' = 60 " (two dashes signify seconds). For
those with nothing better to do, you might note that 1º = 3600". An
object's declination can be given very precisely as, for example,
-34º 27' 41''.
A lot of times astronomers have to keep track of time (not that we
ever have any dates or something like that, but just to keep track of
events in the sky). If astronomers need to talk about minutes and
seconds, like as in units of time, how can we know that they are talking
about time units and not angle units? To distinguish between angular
minutes and seconds and time minutes and seconds, the word arc second or arc minute is often used. You could
say that there are 3600 seconds in a degree, or you could say that there
are 3600 arc seconds in a degree. By using arc seconds people would know
that you are talking about angles and not time.
I should mention that angles are used for not just positions but
also relative positions and angular sizes. What's that mean? You
could say that one object is 10° from another, or you could say that
an object is 10° wide. These are two different things. One is how
far apart two objects appear in the sky (their actual separation may be
quite different). The other is how big an object appears. This is
basically the amount of sky that an object covers. Two big astronomical
objects that you can see with your eye are the Sun and the Moon. How
many degrees across do you think they are? 5°? 10°? Well, you
might be surprised to learn that both are about 1/2° in size! That's
pretty tiny! You don't believe me? Well, take your thumb (you have a
thumb don't you?), hold it at arm's length and place it over the Moon
(this is less painful than holding it over the Sun). Can it cover the
Moon? Your thumb is about 2° across when held at arm's length. Also
try it using a pencil held at arm's length. You might be surprised.
We're going to divert for a moment from the discussion of the
celestial sphere and all that to talk about angles, sizes and distances.
I mentioned that your thumb held at arm's length is about 2° wide.
Why did I have to say "held at arm's length"? What happens if you move
your thumb really close to your eyes? If you are pretty normal, you'll
notice that your thumb looks really big. Does that mean it has a larger
angular size? Yes; your thumb's angular size is now larger. What does
that actually mean? It means that it covers a larger region of your
field of view - it appears bigger. If you could move your thumb further
away, it would look smaller - it would have a smaller angular size
(basically be less than 2° in size). Is your thumb actually changing
its size? No, of course not - not unless you hit it with a hammer
during this process.
This is all rather cute and silly, but what does this have to do
with science and all? Actually, there is a relation between the size of
an object, the distance the object is from you and its angular size. The
relation between these things is
S = R 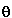 0.0175
0.0175
where S is the actual size of the object (how wide it is), R is the
distance of the object from your eyes and 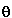 is the angular size (how many degrees
wide it is). This nifty little formula is known as the Small Angle
Formula, since it really only works well for small angles (less than
10º). One of the neat things about this formula is how these
quantities are measured. R and S are in the same units - by this I mean
that if R is measured in inches, then so is S; if S is measured in
kilometers, then so is R; if S is measured in pickles, then so is R; and
so on.
is the angular size (how many degrees
wide it is). This nifty little formula is known as the Small Angle
Formula, since it really only works well for small angles (less than
10º). One of the neat things about this formula is how these
quantities are measured. R and S are in the same units - by this I mean
that if R is measured in inches, then so is S; if S is measured in
kilometers, then so is R; if S is measured in pickles, then so is R; and
so on.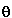 is measured in degrees - you should know
what those are; at least, I hope you do. The number in the formula is
there for making sure everything comes out properly in the end (so that
you end up with the correct units).
is measured in degrees - you should know
what those are; at least, I hope you do. The number in the formula is
there for making sure everything comes out properly in the end (so that
you end up with the correct units).
If you want to actually use this formula, you need to know two out
of three of the things in the formula. For example, if you know that the
Moon is 1/2º in size (= 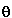 ), and it is 3476 km wide (=S) can you then
determine how far away is it? Just take the formula and determine the
value of R (the distance). The formula is
), and it is 3476 km wide (=S) can you then
determine how far away is it? Just take the formula and determine the
value of R (the distance). The formula is
R = S /(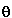 0.0175) = 3476 km / (0.5 x 0.0175) =
397,257 km
0.0175) = 3476 km / (0.5 x 0.0175) =
397,257 km
The Moon is 397,257 km away. Basically, if you know two of the
things, you can always get the third. This is one way to determine the
actual size of an object so long as you know the angular size and the
distance. Conversely, you can get the distance if you know the actual
size and the angular size, or you can get the angular size if you know
the distance and the actual size.
We'll now go back to the coordinates discussion.
How about the East-West designations? We used latitude for the
North-South system, so let's see if we can do the same with longitude
for the East-West coordinates. Unfortunately, we can't use the longitude
system since the objects in the sky move too quickly - they aren't
located constantly over the same location on the Earth. Instead,
astronomers use a system based on a clock. This is logical since it
appears that the sky gets back in the same configuration after 24 hours
(again, you should remember that this is only how it appears; the sky
isn't really rotating!). Astronomers divide the sky into 24 units known
as hours, which go all the way around the Celestial Sphere.
To make your life complicated the name for the East-West coordinate
system is known as Right Ascension (R.A. for short). Values of
R.A. increase as you go further to the east. There is a location
labeled 0h; further east is 1h, then 2h,
... and 22h, then 23h, finally 24h
which is actually the same as 0h. This set up is similar to
how military time is given - numbers increase as you go east until you
are back to where you started from. If you need more precise units, 1h
of R.A. can be divided up into 60 minutes (1h= 60m),
and one minute of R.A. can be divided into 60 seconds (1m=60s).
Note the units of R.A. and dec are different, R.A. has h m s,
while dec has º ' " . An object's full coordinates could be
something like 2º 33' 17'', 14h 7m 33s
- not that you need things so precise all of the time, but if you need
to be that precise this will help you not get lost. Every object
in the sky, not just the stars, but also the planets, the Moon, the Sun
and everything else - can be located at a distinct value of declination
and Right Ascension, just like every location on the Earth can be
designated according to a set of latitude and longitude coordinates. Here is a handy little java
program that allows you to click on a map of the sky to see the
coordinates - I've only included the degrees and minutes values for
declination and the hours and minutes for RA since it is sort of a
rough map. One of the things you'll see is how the RA increases in
value as you go toward the left, which is East in this view.
Star Maps
Often people want to be able to find objects in the night sky, either because it is
a new event, like a comet or supernova, or they just want to know where certain stars
or constellations are located. You can certainly get an atlas of the night sky which is
based upon the the celestial sphere model. Such maps would have the grids of RA and dec
clearly indicated, but such maps may be too much - too detailed. What if you just want to
look at the Big Dipper or find Jupiter? There are various on-line planetarium programs, as
well as apps you can download that can show you what is in the sky, but the classic type of star map is that
which can be printed out and used in the field. These can be found at a variety of sources
including Skymaps.com. These maps take the
entire sky and compress it down to a sheet of paper. Obviously there will be a bit of distortion
in the image. Also since it is a map of what you see when you look up, rather than a map of the Earth
in which you are looking down, the cardinal directions on the map are rather confusing.
Sky maps that show the entire sky usually indicate the time of day and days of the year during
which they are closest to the sky in appearance. Objects at your zenith are at the center of
the map, while along the edges are the various horizons - north, south, east and west. Often
the Milky Way's path is shown, as well as the locations of planets and non-stellar objects that could
be observed with a telescope. If you look at several different star maps, you'll see that the way
that the constellation stick-figures are shown varies slightly - again, the stick figures don't
define the constellation, so there are no rules concerning how they should be drawn.
Objects on the star maps, such as stars and planets, are also shown using dots of different
sizes. The larger dots indicate that the object is brighter, which makes sense. Something that
doesn't make sense is the manner in which astronomers quantify a star's apparent brightness.
Often you'll see a scale showing the dot size and a value labelled as magnitude. You'll
notice that the smaller magnitudes, even the negative values, correspond to the larger dots.
That's something we'll get to in more detail later - a small value of magnitude indicate a very
bright object, while a large value indicates a very faint object. Yes, that is screwy, but that's
the way that astronomers have set things up. Go figure.
Positions of objects relative to the horizon
If you were to sit outside on a clear night, you would notice that
over the course of the evening different objects pass over your head,
and other objects will appear to rise and others will appear to set. If
you were to go outside a month later you would see stars still doing
these things, but the stars wouldn't be in the same places doing the
same things at the same times as you saw them a month ago. A star that
was located near the eastern horizon last month might now be very high
above the southeast horizon at the same time of night. A star you saw in
the west might no longer be visible. When and where stars are located in
the sky varies from night to night. Remember, different constellations
are visible at different times of the year - you'll see why this is in
the next set of notes.
Perhaps you want to see an object when it is highest above the
horizon, as far from the ground as possible. This is the best time to
see an object, since there is less chance that it will be obscured by
trees or buildings, and the atmospheric haze is generally less as you
get further above the horizon. When is an object located furthest from
the horizon? We don't mean just when an object is at your zenith, since
not all objects will pass directly over your head.
The best time to view an object is when it is on your meridian. Like the zenith, the
meridian is a special location, though it is not just a single point. It
is actually a line that runs north-south and passes through your zenith.
When objects are on your meridian, they are at their "highest" location
in the sky. You are most familiar with this when you see the Sun high
up in the sky. It is highest above the southern horizon at about noon.
At this time, it is directly due south of you. If you were to watch
any star or object in the sky and measure its height above the
horizon, you'd notice the largest angle it has above the horizon is
when it is on this north-south line. Check out Figure 5 for an
illustration of this. Another feature of the meridian is that all
objects on your meridian have the same value of R.A. (this is because it
is a line that runs exactly North and South - no part of it is
further to the East than any other part of it). This is the same way
that a line of longitude (which, like the meridian, runs north to
south) acts - all objects on that line have the same value of longitude.
 Figure 5. Meridian
line goes from north to south and passes through your zenith. Objects
on the meridian are at their highest elevation above the ground. If
there was a star on the Celestial Equator, you would see it rise in the
East, be highest above the southern horizon (when it is on your
meridian) then get lower to the ground before it sets in the West.
Figure 5. Meridian
line goes from north to south and passes through your zenith. Objects
on the meridian are at their highest elevation above the ground. If
there was a star on the Celestial Equator, you would see it rise in the
East, be highest above the southern horizon (when it is on your
meridian) then get lower to the ground before it sets in the West.
Now we're going to do some fun things with objects on your meridian
- and believe me, you'll want to pay close attention to this stuff since
you can be guaranteed that it will be on the test. Let's get cracking!
Now remember that at the North Celestial pole you would find the
Pole star (Polaris). Since it is at the Celestial North Pole, it is at a
dec=90º N. Okay, that's pretty easy. If you were to stand on
the Earth's North Pole, Polaris is at your zenith (or you could say
that it is 90º above the horizon). See Figure 6. Being at the
North Pole is not much fun, since it is so dang cold. Let's go somewhere
warmer, like the Equator. If you were to stand on the Earth's Equator,
Polaris is no longer at your zenith, it is on the horizon (or you could
say 0º above the horizon). This is illustrated in Figure 7.
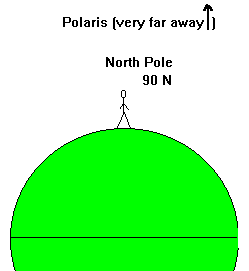
Figure 6. When you are at the North Pole, Polaris is
over your head. |
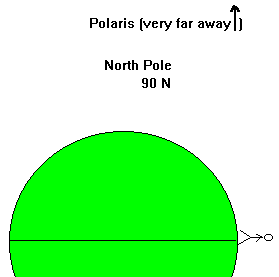
Figure 7. When you are the equator, Polaris is on the
horizon. |
Do you notice a pattern to this? What was your latitude at those
locations? At the North Pole your latitude was 90º N, and Polaris
was 90º above the horizon. At the Equator you latitude was 0º,
and Polaris was located 0º above the horizon (actually it was right
on the horizon). Wow, this is amazing! Your latitude = angle that
Polaris is above the horizon. As long as you can see Polaris, you
can measure its height above the horizon, and that angle will equal
your latitude. Perhaps you can use this information to save your life
someday when you are lost in the woods. All you would have to do would
be to find Polaris, then measure its height above the horizon, and then
you'd know what your latitude was. Perhaps that wouldn't really help
much to save you if you were lost in the woods, but at least you'd be
able to apply something you learned in this class to a real life
experience. Of course in the old days, when navigators used the stars to
sail the seas, the Polaris trick was really helpful. Unfortunately it
only works for Polaris, since there is no star at the Celestial South
Pole.
Let's try the Polaris thing for you at UNI. Remember the latitude of
UNI = 42.5º N, and that means that an object at our zenith is at a
declination of 42.5º N. This means that the Celestial Equator is
located 42.5º south of our zenith. This is shown in Figure
8, which shows the angles and the declinations toward the northern and
southern horizons. If the angle between the zenith and the Celestial
Equator is 42.5º, what is the angle between the Celestial Equator
and the southern horizon? 90 - 42.5 is 47.5º, so the
Celestial Equator is 47.5º above the southern horizon. You may
want to make note of this angle in Figure 8. Let's see what is
happening on the northern side of Figure 8. The difference in
declination between what's at your zenith (dec=42.5º N) and the
North Celestial Pole is 90-42.5=47.5º (hey didn't we see that
number somewhere else?). This is the angle between your zenith and
Polaris - see where that one is in Figure 8. So what is the angle
between the northern horizon and Polaris? Well, it's 90º from the
zenith to the ground, and we already know one angle on the northern
side, so the height of Polaris is just the difference, 90-47.5 =
42.5º. Polaris is 42.5º above the horizon, which is what
I said in the first place! If you are completely confused by this, then
you better read over this section again before we go to the next one,
where you will figure out some other angle problems.
Figure 8. The angles between different points on your meridian.
How to work out those annoying angle problems
Let's look at another problem, similar to the one gone over in the
previous section dealing with how to use the declination values of
objects. All problems like these have 3 parts -
- A latitude
- The declination of an object (how far it is from the Celestial Equator)
- The height above the northern or southern horizon
The diagram that helps you figure out the problem, like that shown in
Figure 8, shows only the northern and southern horizon. Why not the
eastern or western horizon? You might want to think of these problems as
meridian problems, since that is where we are looking at the objects in
the sky, when they are on your meridian (I hope you didn't forget what
the meridian is, because if you did, you may want to look it up again).
Anyways, the diagram just shows the angles along the meridian going from
the ground, the horizon, and extending upwards. You really need to get
your brain around these problems, since they will definitely be on the
test.
Let's go back to the set up in Figure 8, the way that the sky is
oriented along your meridian as viewed from Cedar Falls. How high above
the horizon would an object be if it were on the Celestial equator?
That's an interesting question. First, you should remember that the
Celestial equator is where the declination = 0º, and that location
is shown in Figure 8. Something in that direction would be located
47.5º above the ground when it is on your meridian (also the
greatest height above the horizon).
That was pretty easy; what about an object that is located at a
declination of 33º N? How high above the ground is it? You have to
first determine where that location is in the diagram. Here's one of the
rules you'll need to remember (don't worry I'll summarize these all
later): Declination is measured from the Celestial equator. So
if an object has a declination of 33º N, there must be an angle
equal to 33º between the object and the Celestial equator. But on
which side of the Celestial Equator is the object? Is it to the left or
right of the Celestial equator? Which side has the label
"northern horizon"? That tells you which way is north, so you want to
put the object to the north (or, in this case left) of the Celestial
equator. This is shown in Figure 9. What is the height? 33º +
47.5º (the angle between the object and the Celestial equator added
to the angle between the Celestial equator and the ground) = 80.5º!
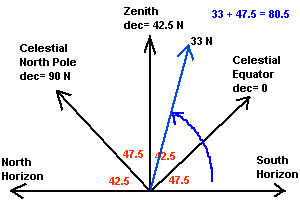 Figure
9. The location of an object along your meridian which has a
declination of 33º North as viewed from Cedar Falls.
Figure
9. The location of an object along your meridian which has a
declination of 33º North as viewed from Cedar Falls.
Here's one that is a bit more confusing - what would the height of
an object be if it has a declination of 80º N? If you follow
the preceding logic, you'd find that it is 52.5º above the northern
horizon. Wait a second, isn't 80º N just 10º away from
the North Celestial pole? Yes, 90-10=80. Okay, so the object is 10°
from the North Star, Polaris. That's fine. Now here's the tricky bit -
how can you be sure of which side of Polaris the object is at? I hate
to admit it, but this is a trick question, since there are actually two
correct answers. How is that possible? You remember those stars
that never set, circumpolar stars? That means at one time they are
found above the North Celestial Pole and at another time they can be
found on the other side, or below the North Celestial Pole, since they
have to go in a circular path around Polaris. This is shown in Figure
10. I'll try to avoid these kinds of questions, since they are
confusing.
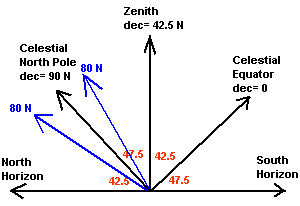 Figure 10. Circumpolar objects can
be found at two locations along your meridian.
Figure 10. Circumpolar objects can
be found at two locations along your meridian.
Let's try another one. What would be the declination of an object
that is located 30º above the Northern horizon when you are located
at a latitude of 15º South. Work on this for a while and once you
have an answer, or if you get completely stumped, just keep reading.
What did you get for an answer? Did you even get an answer? Let's
see how you solve this - and here is where I'll summarize the way that
you tackle these problems.
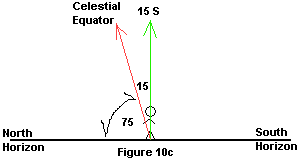
| 1. Make a drawing showing your horizon and your position.
2. Your latitude = the declination of your zenith - so you
know right away one of the declination values of the sky (in this case
you would put 15º S right over your head) - Figure 10a
|
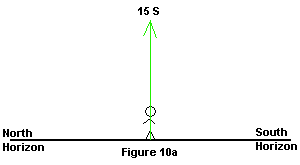 |
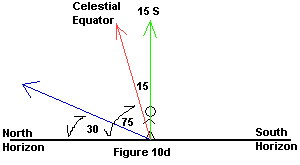
| 3. Figure out where the Celestial equator is - is it to your
north or south? You are in the southern hemisphere (you have a southern
latitude), so the equator is north of you. An easy way to remember this
is to see what the direction of your latitude is; the equator is in the
opposite direction. The Celestial equator is to the left (north) of your
zenith location - Figure 10b shows this. |
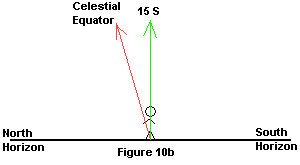 |
| 4. Now put in any of the angles that you can. You know that
the zenith-Celestial equator angle is 15º, since that is how it is
defined (remember, declination is measured from the Celestial equator).
What would be the angle between the Celestial equator line and the
horizon? 90-15=75 left over - remember subtract from 90, not 100! These
angles are shown in Figure 10c. |
 |
| 5. Now you can do anything. If you want to put in the South
Celestial pole and those angles you can, but here you don't need them.
Let's put the object in the picture. What was its location? In case you
forgot, it is 30º above the northern horizon. Is it above the line
marking the Celestial equator? No, since the Celestial equator is
75º up and 30º is much lower than that. Now you can draw it in,
and you better put it below the Celestial equator. You know the angle
between the object and the horizon, since that is what you're given, so
put that in as well. This is shown in Figure 10d. |
 |
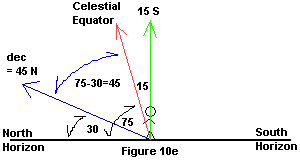
| 6. What is its declination? How is declination measured
or determined? If you haven't figured that out, I'll say it again - declination
is measured from the Celestial equator. How far from the Celestial
equator is the object? Hmm, the Celestial equator is 75º up, the
object is 30º up, so the difference is 75-30=45º. So the
declination is 45º. Is that correct? No it isn't!
I forgot something. Declination is direction dependent - you have to say
North or South. How do you determine if it is North or South? You need
to determine if it is North or South of the Celestial equator. It's to
the left of it, so that means it's North of the Celestial equator. The
final answer is that the object is at a declination of 45º N. Figure
10e shows the final setup. |
 |
If this is what you got, great! If not, well, you should work on it
some more. There are more examples and practice problems available at
this link.
Now that you've read this section, you should be able to answer these questions....
- How do the stars move over the course of an evening?
- What is a celestial sphere used for? Is it realistic?
- What does declination define?
- What does Right Ascension define?
- What can the small angle formula tell you? What do you need to know before you can use it?
- What does the zenith indicate?
- What does the meridian indicate?
- How do you determine the height of an object on your meridian above the horizon?
- How does the declination and your latitude impact the height of objects in the sky?
 What is it? Basically a big see-through imaginary globe
around the Earth. The stars are stuck on this sphere, and as the sphere
spins around, the stars would move with it. This really explains how
the stars move pretty clearly, since they are on this spinning globe,
those near the axis of the rotation, like near the North Star, would make little circles around
the pole star, while those further from the pole
would move along larger paths across the sky. If you don't get this
idea, think about how an umbrella looks as you spin it around above you.
If you have a bunch of spots on the inside of the umbrella, the spots
far from the handle will make large circles around as you rotate the
handle, while those near the handle will make little circles. If you
were to take the ends of the umbrella and stretch them around you would
have a sphere, just like a Celestial Sphere surrounding the Earth.
People thought that the stars' patterns never changed (they stayed in the
same constellation patterns) since they were all "stuck" on this big
sphere. Stars also never appeared to change their appearances, their
colors or their brightnesses - at least not in a way that was
noticeable. By putting them on a fixed, big sphere, people sort of made
them eternal. The worst part of it all is that this model worked really
well! BUT IT IS TOTALLY COMPLETELY WRONG!!! One of the obvious
problems is that it implies that all of the stars are at the same
distance from the Earth, and this is not correct. Even though this model
of the sky is not correct in terms of the real Universe, it is useful
in determining positions of objects and defining a coordinate system of
the sky. Just remember - IT IS WAY WRONG!!!!
What is it? Basically a big see-through imaginary globe
around the Earth. The stars are stuck on this sphere, and as the sphere
spins around, the stars would move with it. This really explains how
the stars move pretty clearly, since they are on this spinning globe,
those near the axis of the rotation, like near the North Star, would make little circles around
the pole star, while those further from the pole
would move along larger paths across the sky. If you don't get this
idea, think about how an umbrella looks as you spin it around above you.
If you have a bunch of spots on the inside of the umbrella, the spots
far from the handle will make large circles around as you rotate the
handle, while those near the handle will make little circles. If you
were to take the ends of the umbrella and stretch them around you would
have a sphere, just like a Celestial Sphere surrounding the Earth.
People thought that the stars' patterns never changed (they stayed in the
same constellation patterns) since they were all "stuck" on this big
sphere. Stars also never appeared to change their appearances, their
colors or their brightnesses - at least not in a way that was
noticeable. By putting them on a fixed, big sphere, people sort of made
them eternal. The worst part of it all is that this model worked really
well! BUT IT IS TOTALLY COMPLETELY WRONG!!! One of the obvious
problems is that it implies that all of the stars are at the same
distance from the Earth, and this is not correct. Even though this model
of the sky is not correct in terms of the real Universe, it is useful
in determining positions of objects and defining a coordinate system of
the sky. Just remember - IT IS WAY WRONG!!!! Figure 1. The
territory that belongs to a certain constellation is shown by the
green lines, while the red lines show a traditional way of drawing the
"shape" of the constellation. The constellation boundaries are not
subject to change, but the lines that represent the stick figure for the
constellation can be drawn in any sort of pattern.
Figure 1. The
territory that belongs to a certain constellation is shown by the
green lines, while the red lines show a traditional way of drawing the
"shape" of the constellation. The constellation boundaries are not
subject to change, but the lines that represent the stick figure for the
constellation can be drawn in any sort of pattern.  Figure 2. The
Celestial Sphere, an imaginary ball around the Earth upon which the
stars were thought to be located. This is not true - the stars aren't
on this sphere, but it does provide an easy way to map out the sky.
Figure 2. The
Celestial Sphere, an imaginary ball around the Earth upon which the
stars were thought to be located. This is not true - the stars aren't
on this sphere, but it does provide an easy way to map out the sky.  Figure
3. The definition of latitude. The angle between your location and
the equator (where latitude =0) determines the value of your latitude.
Figure
3. The definition of latitude. The angle between your location and
the equator (where latitude =0) determines the value of your latitude.  Figure 4. How
declination and latitude are related. An object at your zenith has a
declination value that equals the value of your latitude.
Figure 4. How
declination and latitude are related. An object at your zenith has a
declination value that equals the value of your latitude.  Figure 5. Meridian
line goes from north to south and passes through your zenith. Objects
on the meridian are at their highest elevation above the ground. If
there was a star on the Celestial Equator, you would see it rise in the
East, be highest above the southern horizon (when it is on your
meridian) then get lower to the ground before it sets in the West.
Figure 5. Meridian
line goes from north to south and passes through your zenith. Objects
on the meridian are at their highest elevation above the ground. If
there was a star on the Celestial Equator, you would see it rise in the
East, be highest above the southern horizon (when it is on your
meridian) then get lower to the ground before it sets in the West. 


 Figure
9. The location of an object along your meridian which has a
declination of 33º North as viewed from Cedar Falls.
Figure
9. The location of an object along your meridian which has a
declination of 33º North as viewed from Cedar Falls.  Figure 10. Circumpolar objects can
be found at two locations along your meridian.
Figure 10. Circumpolar objects can
be found at two locations along your meridian. 



