Formula: S = 0.0175 R
Small Angle Formula - This is a relation between distance, size and angular size, and it only works well for small angles, which sort of explains its name.
Formula: S = 0.0175 R ![]() where:
where:
Typical Problems
1. An object with a diameter of 38 cm is located 688 m away. What is its angular size?
Solution: You'll need to rearrange the formula, since you have to solve for ![]()
S = 0.0175 R ![]()
![]() = S/(0.0175 R)
= S/(0.0175 R)
Since S and R must be in the same units of measure, the value of S will be converted to meters, so S = 38 cm = 0.38 m
![]() = 0.38 / (0.0175 x 688) = 0.032 degrees.
= 0.38 / (0.0175 x 688) = 0.032 degrees.
2. An object is located 45 km away. If its angular size is 2.0 degrees, what is its actual size?
Solution: You don't have to rearrange the formula since you are looking for the value of S, therefore
S = 0.0175 R ![]()
S = 0.0175 x 45 x 2.0 = 1.6 km
3. If an object is 25 cm in size, and it has an angular size of 15 arcminutes, how far away is it?
Solution: You'll have to rearrange the formula to solve for R.
S = 0.0175 R ![]()
R = S /(0.0175 ![]() )
)
And you also have to convert the angle into degrees. 1 degree = 60 arcminutes, so the angle in this problem is 0.25 degrees.
R = 25 / (0.0175 x 0.25) = 5700 cm.
Angle Problems - These are those annoying angle problems that you enjoy so much. There is no actual formula but a well defined procedure that should be followed to solve them. Each of the problems has 3 parts, your latitude, the declination of an object and its height above the horizon when it is on the meridian. You are given two of these and then you have to find the third.
Procedure: Follow these steps -
Typical Problems
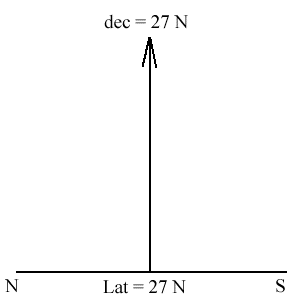
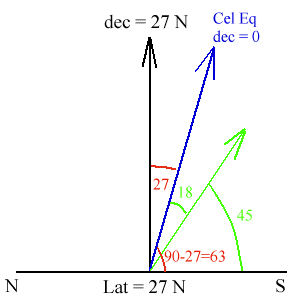
1. You are at a latitude of 27 degrees north and there is an object with a declination of 18 S. How high above the horizon is it when it is on your meridian?
Solution: You need to follow the steps carefully.
Your latitude = declination at your zenith - this is pretty easy, just put in your latitude and you have what the declination is for a point directly above your. This is shown below
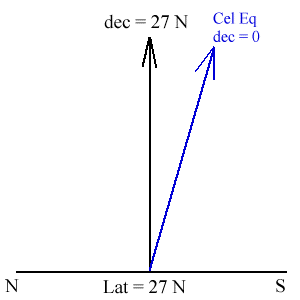
Put in the celestial equator - since you are in the north, the celestial equator is to the south of you. So put that in. You have to have the celestial equator in since all declinations are measured relative to it - it is a very important location. This is shown below
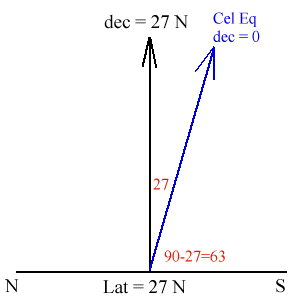
Put in the angles between the various direction that you have so far - this is always vital so you can be set up before doing the last bits. You have the angle between your zenith and the celestial equator which is just 27 - 0 =27. You also have the angle between the celestial equator and the ground, which is 90-27 = 63 degrees. This is shown below.
Put the object in - now you finally get to do the last thing, putting in the object. You have that the object is at a declination of 18 S. This means it is 18 degrees south of the celestial equator, or in this case, 18 degrees below the celestial equator. Put it in and since you already know that the celestial equator is 63 degrees above the ground, the object is 63 - 18 = 45 degrees above the southern horizon. This is shown below.
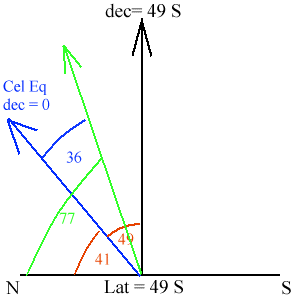
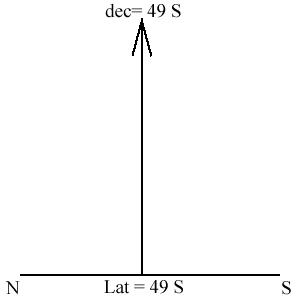
2. You are at a latitude of 49 S. You see an object that is 77 degrees above the northern horizon. What is the object's declination?
Solution: Again follow the steps -
Your latitude = declination at your zenith - this is pretty easy, just put in your latitude and you have what the declination is for a point directly above your. This is shown below
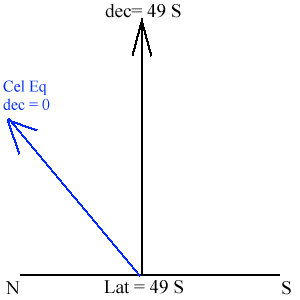
Put in the celestial equator - since you are in the south, the celestial equator is to the north of you. So put that in. You have to have the celestial equator in since all declinations are measured relative to it - it is a very important location. This is shown below
Put in the angles between the various direction that you have so far - this is always vital so you can be set up before doing the last bits. You have the angle between your zenith and the celestial equator which is just 49 - 0 =49. You also have the angle between the celestial equator and the ground, which is 90-49 = 41 degrees. This is shown below.
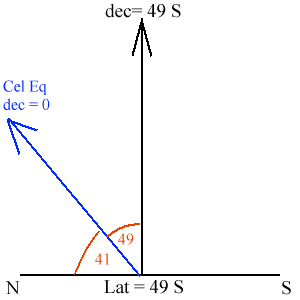
Put the object in - now you finally get to do the last thing, putting in the object. You have that the object is located 77 degrees above the northern horizon. This places it above the celestial equator in your diagram. When you have it in there you need to determine its declination. How do you do that? You have to remember, declination is measured relative to the celestial equator. So how far is the object from the celestial equator? Well the celestial equator is 41 degrees above the ground and the object is 77 degrees up, so the object is 77 - 41 = 36 degrees from the celestial equator. So the declination of the object is 36 degrees, right? Nope, you have to include a direction. Is it north or south of the celestial equator? It is to the right of it, and in this diagram, right is the direction of south, so it is south of the celestial equator. Therefore the object's declination is 36 S This is shown below.